pythonでサポートベクターマシン(SVM)で回帰モデルを構築

こんにちは、デジタルボーイです。今回はサポートベクターマシン（SVM）で回帰モデルをPythonとscikit-learnを使って構築したいと思います！

記事を書いた人

デジタルボーイです。
データサイエンス歴20年以上のおっさんです。中小企業診断士として、データサイエンス、WEBマーケティング、SEOに関するデータ分析、コンサルティングの仕事をしています。自己紹介の詳細はコチラ

サポートベクターマシン（回帰）とは？

サポートベクターマシン（SVM）は、元々は分類問題を解くためのアルゴリズムですが、回帰問題にも応用できます。回帰版のSVMは「サポートベクター回帰（SVR）」と呼ばれ、データの分布に対して最も誤差が小さくなるような「マージン」内に収める回帰モデルです。以下のような特徴を持っています。

• ロバストな回帰
  • 外れ値に強く、過学習しにくい
• カーネル法による非線形回帰
  • 非線形な関係も捉えることが可能（例：RBFカーネルを使う）
• ε（イプシロン）による誤差の調整
  • 許容誤差（ε）内にデータ点を収めるように最適化

直感的な理解

以下のようなグラフを考えてみましょう。

• 線形SVR: データが直線的に並ぶ場合、SVRは直線を引いて近似します。
• 非線形SVR: データが曲線的な傾向を持つ場合、RBFカーネルを使うことで曲線的な回帰が可能です。

たとえば、次のようなグラフが代表的なアウトプットです。

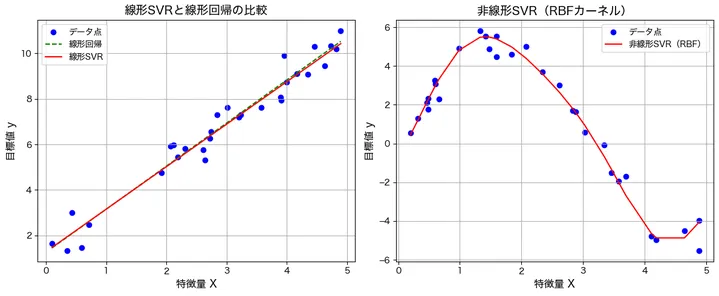
左のグラフでは、線形SVRと線形回帰の違いを示しています。線形回帰は、データのばらつきを考慮せずに、誤差を最小化する1本の直線を引いています。一方、線形SVRは、一定の誤差範囲（マージン）の中にデータ点を収めようとするため、線形回帰とは若干、異なる直線を描いています。線形SVRでは、誤差が許容範囲内であれば修正しないため、一部のデータ点に影響を受けにくい特徴があります。そのため、線形回帰よりも外れ値の影響を抑えた回帰モデルとなることがわかります。

右のグラフでは、非線形SVR（RBFカーネル）を適用した場合の回帰結果を示しています。データが曲線的な関係を持つ場合、単純な直線では適切に予測できません。しかし、RBFカーネルを用いることで、非線形なデータにも対応し、曲線的な回帰モデルを構築できます！このグラフでは、赤い線がデータの変化に沿って滑らかな曲線を描いており、RBFカーネルがデータのパターンを適切に捉えていることがわかります。非線形SVRは、特に複雑な関係を持つデータに対して有効であり、線形モデルよりも高い精度を実現できるケースが多いです。

サポートベクター回帰の応用場面

サポートベクターマシンは次のような場面で利用されます。

必要なライブラリのインポート

SVRを使うには、scikit-learnライブラリを利用します。まだインストールしていない場合は、以下のコマンドでインストールしてください

pip install scikit-learn numpy matplotlib

pipを使ったインストール方法がわからない場合はこちらをご覧ください。

あわせて読みたい

pipでpandasをインストールする方法 こんにちは、デジタルボーイです。備忘録がてら、macとLinuxにpipでpandasをインストールするための手順を、まとめておきます。 記事を書いた人 デジタルボーイです。デ…

あわせて読みたい

pipでnumpyをインストールする方法 こんにちは、デジタルボーイです。備忘録がてら、macとLinuxにpipでNumPyをインストールするための手順を、まとめておきます。 記事を書いた人 デジタルボーイです。デ…

あわせて読みたい

pipでscikit-learn(sklearn)をインストールする方法： こんにちは、デジタルボーイです。備忘録がてら、macとLinuxにpipでscikit-learn(sklearn)をインストールするための手順を、まとめておきます。 記事を書いた人 デジタ…

では、必要なライブラリをインポートしましょう。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

これで準備完了です！次に、実際にSVRを使ったモデルの実装を行いましょう。

データ概要の確認

サポートベクター回帰（SVR）を実装するために、scikit-learn のデータセットからサンプルデータを使用します。ここでは、sklearn.datasets に含まれる Boston Housing Dataset を使用します。これは、ボストン市の住宅価格を予測するためのデータセットであり、各住宅の価格とそれに影響を与えるさまざまな特徴量が含まれています。特徴量には、犯罪率や部屋数、空気汚染レベルなどが含まれています。

まずは、データをロードして、どのようなデータが含まれているのかを確認しましょう。

from sklearn.datasets import fetch_california_housing
import pandas as pd

# データのロード
data = fetch_california_housing()

# データをPandasのDataFrameに変換
df = pd.DataFrame(data.data, columns=data.feature_names)
df["Target"] = data.target

# データの先頭5行を表示
df.head()

結果はこうでした。

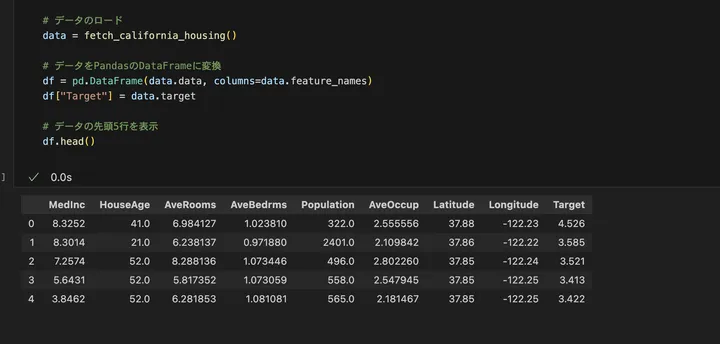
今回のデータには、住宅価格を予測するためのいろんな特徴量が含まれてそうですね！「MedInc（中央値所得）」 はその地域の住民の平均所得を示し、経済的な背景を反映しています。「HouseAge（築年数）」 は住宅の築年数を示し、新築か古い住宅かを判断する指標となります。「AveRooms（平均部屋数）」や「AveBedrms（平均寝室数）」 は住宅の広さや部屋の構成を示し、間取りの特徴を表します。「Population（人口）」 はその地域の人口規模を示し、居住環境の特徴を把握するのに役立ちます。「AveOccup（平均居住者数）」 は1戸あたりの平均居住人数を表し、住宅の利用状況を示す指標となります。さらに、「Latitude（緯度）」と「Longitude（経度）」 は住宅の地理的な位置を示し、どのエリアにあるかを把握するための情報となります。

分析の目的とゴール

本分析では、サポートベクター回帰（SVR）を用いてカリフォルニア州の住宅価格を予測することを目的とします。住宅価格は、多くの要因によって変動するため、単純な線形回帰では表現しきれない可能性があります。そのため、SVRを用いることで、非線形な関係を考慮した精度の高い予測モデルを構築することを目指します。

具体的なゴールを挙げてみます！

1. カリフォルニアの住宅価格を予測できるSVRモデルを構築する
2. モデルの予測精度を評価し、適切なパラメータを調整する
3. 他の回帰モデルと比較し、SVRの特徴を理解する

SVRがどの程度住宅価格の予測に適しているのかを実験し、実際の活用に向けた知見を得ることが最終的な目標です。さあ、モデルを作ってみましょう！

モデルの実装

データの前処理を行い、SVRを用いた回帰モデルを構築します。

import time
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVR

# データの分割
X = df.drop("Target", axis=1)
y = df["Target"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 特徴量のスケーリング
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# SVRモデルの構築
svr = SVR(kernel="rbf", C=100, epsilon=0.1)

# 学習と推定時間の計測
start_time = time.time()
svr.fit(X_train_scaled, y_train)
y_pred = svr.predict(X_test_scaled)
end_time = time.time()

# 推定時間の出力
elapsed_time = end_time - start_time
print(f"推定にかかった時間: {elapsed_time:.3f} 秒")

結果はこうでした。

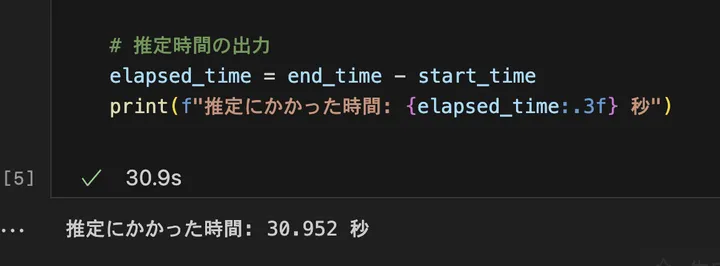
私のMacbook Proで30秒ほどかかりましたが、これで、SVRによる住宅価格の予測モデルが完成しました！次は、モデルの評価と改善に進みます。

モデルの評価

サポートベクター回帰（SVR）の性能を評価するために、以下の指標を使用します。

1. MSE（Mean Squared Error: 平均二乗誤差）
   予測値と実際の値の誤差を二乗し、それを平均したものです。値が小さいほど予測精度が高いことを示します。単位が元のターゲット変数の二乗になるため、解釈しづらい点が難点です。
2. RMSE（Root Mean Squared Error: 平均二乗誤差の平方根）
   MSEの平方根を取ることで、元のターゲット変数と同じ単位になります。MSEよりも解釈しやすく、一般的に回帰モデルの誤差評価に使われます。
3. R²（決定係数）
   予測モデルがどの程度データのばらつきを説明できているかを示す指標です。値は0から1の範囲を取り、1に近いほど良いモデルといえます。負の値になる場合、モデルの性能が非常に悪いことを意味します。

これらの評価指標を計算し、SVRモデルの精度を確認しましょう！

from sklearn.metrics import mean_squared_error, r2_score
import numpy as np

# MSE, RMSE, R2の計算
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
r2 = r2_score(y_test, y_pred)

# 結果を出力
print(f"平均二乗誤差 (MSE): {mse:.3f}")
print(f"平均二乗誤差の平方根 (RMSE): {rmse:.3f}")
print(f"決定係数 (R²): {r2:.3f}")

結果はこうでした。

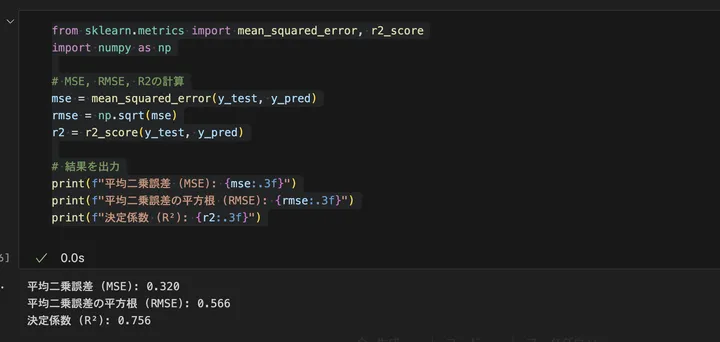
今回のSVRモデルの評価結果は以下のとおりです。

• MSE（平均二乗誤差）: 0.320
  これは、予測値と実際の住宅価格の二乗誤差の平均です。値が小さいほど誤差が少なく、良いモデルといえますが、MSEは単位が二乗されているため、直接の解釈は難しいです。
• RMSE（平方根平均二乗誤差）: 0.566
  RMSEを使うと、誤差の平均的な大きさを住宅価格の単位で見ることができます。この場合、モデルの予測は平均して 0.566（数千ドル単位） ほどズレていることになります。住宅価格のスケールを考えると、まずまずの精度といえます。
• R²（決定係数）: 0.756
  R² の値が 0.756 ということは、住宅価格の変動の 約75.6% を説明できていることを意味します。一般的に、R² が 0.7 以上 であれば「それなりに良いモデル」と評価できます。とはいえ、完全にデータの傾向を捉えられているわけではなく、もう少し精度を上げる余地があります。

今回のSVRモデルは、住宅価格をそこそこの精度で予測できています。MSEやRMSEの値も大きすぎず、R² も 0.7 を超えていることから、一定の説明力があるといえるでしょう！

モデルのグラフ化

続いて、推定した予測値と実測値の関係を散布図で見てみましょう。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import pearsonr

# フォント設定（Mac用）
plt.rcParams["font.family"] = "Hiragino sans"

# 実測値と予測値の相関係数を計算
correlation, _ = pearsonr(y_test, y_pred)

# 散布図の描画（横軸: 実測値, 縦軸: 予測値）
plt.figure(figsize=(8, 6))
plt.scatter(y_test, y_pred, alpha=0.6, color="blue", label="予測値")
plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], linestyle="--", color="red", label="理想線")

# グラフの設定
plt.title(f"実測値と予測値の関係（相関係数: {correlation:.3f}）", fontsize=14)
plt.xlabel("実測値", fontsize=12)
plt.ylabel("予測値", fontsize=12)
plt.legend()
plt.grid(True)

# グラフの表示
plt.show()

結果はこうです。

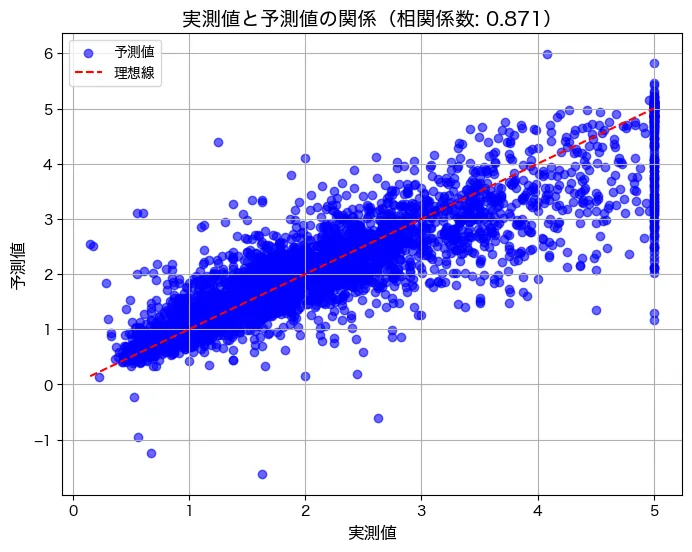
実測値はおそらく1０万ドル単位でしょう。データは50万ドルを上限にぶったぎられています。50万ドルのぶった斬りを無視すれば、概ね実際の住宅価格が上がるにつれて、予測値も上がっており、良い関係であると言えます。相関係数も0.87と非常に高い相関がありました！

モデルが予測したパラメータの出力と解釈

サポートベクター回帰（SVR）は、線形回帰のように明確な「回帰係数（重み）」を持ちません。とはいえ、「Permutation Importance（置換重要度）」 を使うことで、各特徴量が予測にどれだけ影響を与えているかを測定できます。ちなみに、これはSVR特有の技術ではなく、他のモデルにも利用できます。また、回帰モデルだけでなく、2値モデルにも利用可能です。

Permutation Importance（置換重要度）で重要度を算出

from sklearn.inspection import permutation_importance

# 置換重要度の計算
result = permutation_importance(svr, X_train_scaled, y_train, scoring='r2')

# 特徴量ごとの重要度を出力
for feature, importance in zip(data.feature_names, result.importances_mean):
    print(f"{feature}: {importance:.4f}")

結果はこうでした。

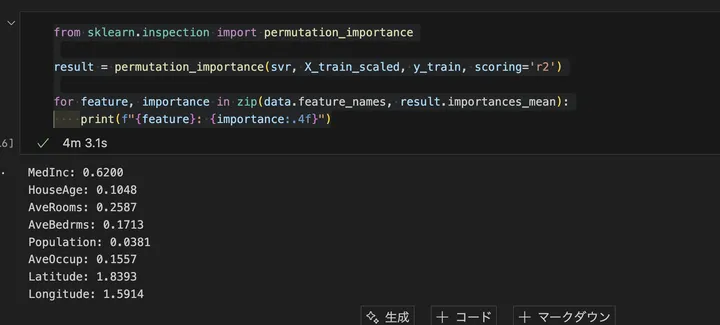
また、実行時間は4分でした。なかなか使いづらいぞ！ちなみに、今回はR²を使いましたが、それ以外にも、以下のように、いろいろな指標を選択できます。

では、具体的にモデルの結果を解釈してみましょう！！

この結果を見ると、「Latitude（緯度）」と「Longitude（経度）」が最も重要な特徴量 であることが分かります。これは、カリフォルニア州の住宅価格が 地理的な要因に大きく依存している ことを示しています。例えば、サンフランシスコやロサンゼルスのような都市部では住宅価格が高く、地方では安くなる傾向があります。緯度と経度が価格に強い影響を与えているのは、立地の影響が大きい証拠といえます。

次に影響が大きいのは 「MedInc（中央値所得）」で 0.6184 となっています。これは、住民の所得が高い地域では住宅価格も高くなる傾向がある ことを示しています。一般的に、所得の高いエリアは不動産価格も高く、逆に所得の低い地域では価格が低くなります。この結果は、住宅市場の基本的な経済原理を反映しています。

「AveRooms（平均部屋数）」と「AveBedrms（平均寝室数）」 もある程度の影響を持っており、それぞれ 0.2517 と 0.1703 という値になっています。これは、部屋数や寝室数が多い住宅は価格が高くなりやすいことを示唆しています。ただし、経度や緯度、所得ほどの影響はなく、相対的に影響度は中程度であることが分かります。

ということで、住宅価格の決定には、「立地（緯度・経度）」と「住民の所得」が最も大きく影響を与えている ことが分かりました！部屋数や寝室数も影響を持ちますが、立地や所得と比べると影響度は低めです。築年数や人口の影響はさらに小さく、住宅価格を予測する上ではそこまで重要な要因ではない可能性があります。これは、カリフォルニア州の住宅市場が「立地と所得によって大きく決まる」ことを示しており、不動産価格の現実的な傾向と一致していましたね！

sklearnのカーネル（kernel）について：どれを選ぶべきか？

サポートベクター回帰（SVR）では、カーネル（kernel） を選択することで、データの特徴をどのように学習するかが決まります。カーネルは、入力データを高次元に変換し、線形では表現できない関係を学習するための関数 です。

主なカーネルの種類と選び方

まとめ

以上、サポートベクターマシンにおける回帰モデル、SVRについて解説しました。SVRは、線形回帰では捉えきれない複雑な関係を学習できる強力なモデルです。特に、RBFカーネルを用いることで、非線形なデータのパターンを捉え、高精度な予測が可能になります。一方で、今回の分析例でもみましたが、計算コストが高く、大規模データには向かない点には注意が必要です。

また、SVRは決定木系のモデルのように特徴量の重要度を直接取得できませんが、Permutation Importanceを活用することで、どの特徴量がモデルの予測に影響を与えているかを分析できます。今回の例では、カリフォルニア住宅価格のデータを用い、立地（緯度・経度）や住民の所得が特に重要であることが分かりました。

SVRを実務で活用する際は、カーネルの選択やハイパーパラメータの調整を適切に行い、データの特性に合ったモデルを構築することが重要です。