こんにちは、デジタルボーイです。今回は予測精度をあげるための特徴量エンジニアリングについて、Pythonプログラミングを使いながら解説したいと思います。

デジタルボーイです。
データサイエンス歴20年以上のおっさんです。中小企業診断士として、データサイエンス、WEBマーケティング、SEOに関するデータ分析、コンサルティングの仕事をしています。自己紹介の詳細はコチラ
予測モデルの精度を高めるカギ、特徴量エンジニアリング
機械学習や統計モデルで「精度を上げたい!」と思ったとき、最初に頭に浮かぶのはアルゴリズムの選定やハイパーパラメータの調整かもしれません。でも、個人的には、それ以上に効果があると言われているのが特徴量エンジニアリング(Feature Engineering)です。
特徴量エンジニアリングとは、モデルに与える入力データ(特徴量)を工夫して変換・生成・選別するプロセスです。モデルの学習は、この特徴量に大きく依存するため、良い特徴量を作ることができれば、単純なモデルでも驚くほど高精度な予測が可能になることがあります。
例えば、ある商品の売上を予測する場合に、単に「価格」や「天気」だけを使うのではなく、「週末かどうか」や「過去7日間の平均売上」など、より意味のある特徴を作ることで、モデルの理解力が一気に高まります。
データ分析では「ゴミを入れれば、ゴミが出てくる(Garbage in, Garbage out)」という格言があります。つまり、モデルに渡す特徴量の質が低ければ、どんなに最新のAI技術を使っても良い結果は得られないというわけです!
本記事では、この特徴量エンジニアリングについて、予測モデルの精度向上という観点からわかりやすく解説していきます。初学者の方でも安心して読み進められるよう、Pythonの基礎コードとともにやさしく説明していきますね。欠損値と外れ値の処理
まず初めに欠損値と外れ値の処理をする必要があります。基本的には欠損値の処理は、①は必須で実施し、余裕があれば②もやる、という流れでいいでしょう。
- 平均/中央値/最頻値で補完
- 欠損の有無を示すフラグ変数の追加
また、外れ値については以下の4つのうちのどれかの対処をします。
- 行ごと削除する
- 上限・下限を設定(クリッピング)する
- 変換する(ロジスケール・対数変換など)
- 「異常値」と「それ以外」といったカテゴリ列を追加する
また、欠損値と外れ値についての詳しい対処法についてはこちらに解説してあるので、よかったら参考にしてください。

カテゴリ変数の処理
予測モデルを作るときに、よく出てくるのがカテゴリ変数です。カテゴリ変数とは、例えば「曜日」や「天気」など、数字ではなくラベル(文字列など)で表される変数のことです。こうしたデータはそのままでは数値を扱う機械学習モデルに使えないため、前処理によって数値に変換する必要があります。
ここでは、カテゴリ変数を扱う代表的な方法として、以下の3つを紹介します:
- ラベルエンコーディング
- One-hotエンコーディング
- ターゲットエンコーディング(平均目的変数)
それぞれ、Pythonのコードと一緒に解説します!
カテゴリ変数への対応1:ラベルエンコーディング
ラベルエンコーディングは、カテゴリごとに整数を割り振る方法です。例えば「晴れ」「曇り」「雨」を、以下のようにそれぞれ 0, 1, 2 のように変換します。
| 天気 | 天気_encoded |
|---|---|
| 晴れ | 2 |
| 曇り | 0 |
| 雨 | 1 |
| 晴れ | 2 |
ラベルエンコーディングはとても簡単に使えるため、つい多用してしまいたくなります。でも、実はモデル構築の際には注意すべき重要なポイントがあります。
というのも、ラベルエンコーディングは、カテゴリごとに「0」「1」「2」…のような連番の整数値を割り当てるだけの手法です。そのため、カテゴリ同士に“数値的な順序”があるとモデルに勘違いされてしまうことがあります。
例えば、「天気」というカテゴリが sunny = 2, cloudy = 0, rainy = 1 とラベルエンコーディングされたとしましょう。これを使ってモデルを学習させると、モデルは「cloudy < rainy < sunny」という大小関係や距離感を読み取ってしまう可能性があります。でも、実際には天気のラベルに数値的な順序なんて存在しません。晴れが曇りより「2倍すごい」わけでも、「1だけ上」なわけでもない!、ということです。
この誤解が原因で、モデルが不適切なルールを学習してしまい、精度が落ちることがあります。特に線形モデル(線形回帰やロジスティック回帰)では影響が大きく出やすいです。
そのため、カテゴリに意味のある順序がない場合は、ラベルエンコーディングではなく、One-hotエンコーディングのような順序を持たない方法を選ぶ方が安全です。
カテゴリ変数への対応2:One-hotエンコーディング
One-hotエンコーディングは、各カテゴリを新しい列に分解して、該当する列だけ1、他は0にする方法です。カテゴリの数が少ない場合に有効です。以下は天気という列をOne hotエンコーディングした例です。
| 天気 | 曇 | 雨 | 晴 |
|---|---|---|---|
| 晴 | 0 | 0 | 1 |
| 曇 | 1 | 0 | 0 |
| 雨 | 0 | 1 | 0 |
| 晴 | 0 | 0 | 1 |
この方法は安全ですが、カテゴリ数が多いと列が増えすぎてしまう(次元の呪い)ことがあります。その結果、学習データの情報が疎になり、モデルが過学習しやすくなるリスクが高まります。例えば、「都道府県」というカラムがあると47個分の列がone hotによい作られ、「市区町村」というカラムがあると1000以上のカラムが一気に作成されてしまう恐れもあります。
とくに決定木などの木系モデルではあまり影響が出ませんが、線形モデルや距離ベースのアルゴリズムでは性能に悪影響を及ぼすこともあります。カテゴリ数が多い場合は、頻度の低いカテゴリを「その他」とまとめたり、次で紹介するターゲットエンコーディングなど別の方法を検討するのが有効です。
カテゴリ変数への対応3:ターゲットエンコーディング
ターゲットエンコーディングは、各カテゴリに対応する目的変数(ターゲット)の平均値を使って数値化する手法です。例えば「日曜の売上は平均1100円、月曜は750円…」というように、ラベルごとのターゲット平均でエンコードします。
| 曜日 | 売上 | 曜日_エンコード |
|---|---|---|
| 日曜 | 1000 | 1100 |
| 月曜 | 800 | 750 |
| 日曜 | 1200 | 1100 |
| 火曜 | 900 | 900 |
| 月曜 | 700 | 750 |
この方法は、予測に有効な情報を取り込めるというメリットがありますが、学習用データと検証用データの間で情報漏洩(リーク)が起きやすいので注意が必要です。
ターゲットエンコーディングでは、あるカテゴリに対して目的変数(たとえば売上など)の平均値を使って数値化します。とても便利な方法ですが、気をつけないと「未来の情報」を使ってしまう危険があります。たとえば、モデルの予測を試すためのテスト用データまで含めて平均を計算してしまうと、モデルがまだ見ていないはずの売上情報をこっそり知ってしまうことになります。これでは、本来の実力よりも良いスコアが出てしまい、本番でうまく動かないモデルができてしまうかもしれません。
これを防ぐには、例えば、モデルの練習用のデータだけで平均を計算して、テスト用のデータにはその結果だけを使うというルールを守ることが大切です。少し注意が必要な方法ですが、正しく使えばとても効果的な方法です!
スケーリング・正規化
データ分析や機械学習において、「スケーリング」や「正規化」と呼ばれる前処理はとても重要です。というのも、多くのアルゴリズムでは、特徴量のスケール(数値の大きさの単位)が揃っていないと、正しく学習できないからです。
たとえば、ある特徴量が0〜1の範囲で、別の特徴量が1000〜10000の範囲にあると、数値の大きい特徴量に引っ張られてしまい、バランスの悪いモデルになってしまうことがあります。
スケーリングは、こうした特徴量の数値の幅を調整して、アルゴリズムがすべての特徴量を公平に扱えるようにする作業です。ここでは、よく使われる3つの手法をご紹介します!
Min-Maxスケーリング
Min-Maxスケーリングは、データを0から1の範囲におさめる方法です。最小値を0、最大値を1として、すべての値をその範囲内に再配置します。
| 年齢 | 年齢_スケーリング |
|---|---|
| 18 | 0 |
| 25 | 0.166 |
| 30 | 0.285 |
| 45 | 0.642 |
| 60 | 1 |
この手法は、すべてのデータを同じスケールで扱えるため、画像処理やニューラルネットワークの入力などに向いています。ただし、外れ値(極端に大きい・小さい値)があると、スケールが崩れてしまうので注意が必要です。
標準化(Zスコア)
標準化は、平均を0、標準偏差を1に変換する方法です。つまり、値が平均からどれだけ離れているかを「標準偏差の単位」で表現します。
| 年齢 | 年齢_標準化 |
|---|---|
| 18 | -1.167 |
| 25 | -0.702 |
| 30 | -0.371 |
| 45 | 0.623 |
| 60 | 1.6179 |
この方法は、正規分布に近いデータに対して特に効果を発揮し、線形回帰やロジスティック回帰、SVMなどで安定した学習が可能になります。Min-Maxと違って、外れ値の影響を受けにくい点も特徴です。
対数(ログ)変換(右に歪んだ分布への対応)
売上やアクセス数など、「小さい値が多くて、大きい値が少しだけある」ようなデータは、右に大きく尾を引いた形の歪んだ分布になります。このようなデータは、そのまま使うとモデルの学習が難しくなってしまうことがあります。
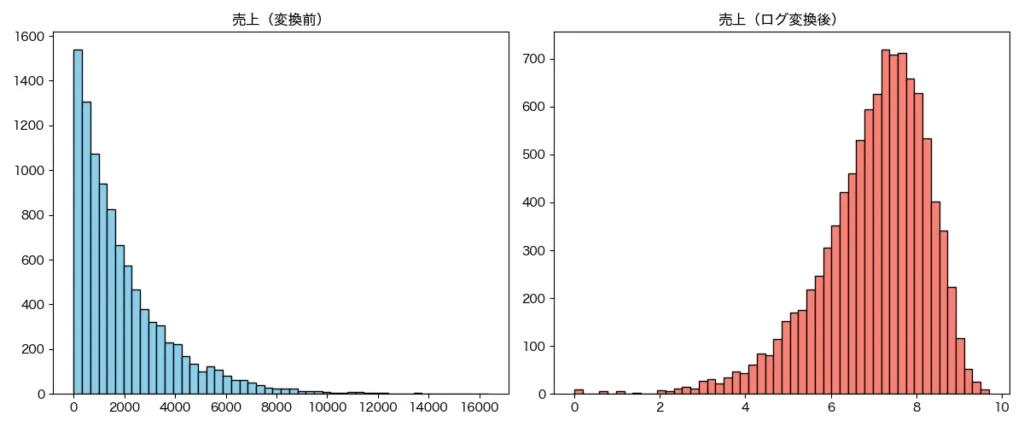
そこで使えるのがログ変換です。値の大きさの差を圧縮して、分布をぐっと平らにすることができます。これにより、極端に大きな値が悪さをせず、モデルが安定して学習しやすくなるというメリットがあります。
組み合わせ・変換による特徴量生成
特徴量エンジニアリングでは、元のデータをそのまま使うだけでなく、組み合わせたり変換したりすることで、より予測に役立つ新たな特徴量を作ることができます。これは、予測精度を上げるためにとても効果的なアプローチのひとつです。
ここでは、代表的な特徴量生成の方法をいくつか紹介します。どれも、実際の分析現場でよく使われるテクニックです!
特徴量の加減乗除による組み合わせ
数値データが複数ある場合、その足し算・引き算・掛け算・割り算によって新しい情報を作り出すことができます。
たとえば「単価(A)」と「数量(B)」がある場合、A × B で「売上金額」が得られます。あるいは A ÷ B によって、何かの比率を作ることもできます。こうした新たな意味を持つ特徴量は、モデルの理解を助け、精度向上に貢献することが多いです。
| 単価 | 数量 | 売上金額 | 単価差 | 数量比 |
|---|---|---|---|---|
| 100 | 1 | 100 | nan | nan |
| 150 | 2 | 300 | 50 | 2 |
| 200 | 3 | 600 | 50 | 1.5 |
| 250 | 4 | 1000 | 50 | 1.33333 |
| 300 | 5 | 1500 | 50 | 1.25 |
この出力では、「単価」と「数量」から「売上(掛け算)」、「単価差(前の行との引き算)」、「数量比(前の行との割り算)」といった加減乗除による新しい特徴量を生成した例を示しています。
ただし、意味のある計算かどうかをよく考えることが大切です。何でも組み合わせれば良いというわけではありません!
ビン化(binning)
数値をそのまま扱うのではなく、区切ってグループに分ける方法です。たとえば年齢を「10代」「20代」「30代」といったように分けると、人の属性に近い意味を持つことができます。
| 年齢 | 年代 |
|---|---|
| 15 | 10代以下 |
| 22 | 20代 |
| 27 | 20代 |
| 34 | 30代 |
| 45 | 40代 |
| 52 | 50代 |
| 63 | 60代 |
| 78 | 70代以上 |
この出力では、「年齢」データをもとに、10代以下〜70代以上といった年代のカテゴリに分けるビン化(binning)の例を示しています。
また、四分位数(全体を4つに分ける)や、任意の分位点で区切ることで、極端な値の影響を抑えながら傾向を捉えることができます。分類問題では、こうしたビン化がとても有効なケースも多いです!
日付データからの抽出
日付や時刻が含まれるデータは、そのまま使うよりも、意味のある要素を取り出して使う方が効果的です。たとえば:
- 曜日(平日か週末か)
- 月(季節性の把握に有効)
- 四半期(ビジネスサイクルの分析に便利)
- 時間帯(午前/午後、深夜など)
- 祝日かどうか
こういった情報を取り出すことで、時間にまつわる傾向をモデルに学習させることができます。
| 注文日 | 曜日 | 月 | 四半期 | 週末フラグ |
|---|---|---|---|---|
| 2024-04-01 | 月曜 | 4 | 2 | False |
| 2024-04-06 | 日曜 | 4 | 2 | True |
| 2024-05-15 | 水曜 | 5 | 2 | False |
| 2024-06-22 | 土曜 | 6 | 2 | True |
| 2024-07-07 | 日曜 | 7 | 3 | True |
この出力では、「注文日」から曜日・月・四半期・週末フラグ・時間帯といった特徴を抽出し、時間に関する傾向をモデルが学習しやすくする処理を表しています。
経過日数(例:ある日からの差分)
たとえば「会員登録してから何日経ったか」「購入日からの経過日数」など、基準日との差を計算する特徴量は、時間の流れに伴う変化を捉えるのにとても役立ちます。
| 注文日 | 経過日数 |
|---|---|
| 2024-04-01 | 0 |
| 2024-04-05 | 4 |
| 2024-04-10 | 9 |
| 2024-04-20 | 19 |
| 2024-05-01 | 30 |
この出力では、「注文日」と基準日(ここでは4月1日)との差から経過日数を算出しており、時間の流れによる変化を捉えるための特徴量として活用できます。
時間が経つことでユーザーの行動や状態が変わるようなケースでは、このような経過時間の特徴量が非常に強力になります!
テキストデータの変換
テキストはそのままだと扱えないため、数値的な形に変換する必要があります。よく使われる方法には以下があります:
- Bag-of-Words:単語の出現回数を特徴量にする
- TF-IDF:よく出るが他と被らない単語を重視する
- Word2Vec:単語の意味や関係性をベクトルで表現する
また、テキストの長さや単語数、記号の数なども、単純ですが重要なヒントになることがあります。たとえば、「レビューがやたら長い」「!が多い」などは感情の強さを表しているかもしれません。
| レビュー | 文字数 | 単語数 | 感嘆符数 |
|---|---|---|---|
| とても美味しかった!また行きたいです。 | 19 | 1 | 1 |
| 味は普通。接客が少し残念でした。 | 16 | 1 | 0 |
| 量が多くて満足。コスパ最高! | 14 | 1 | 1 |
| 期待外れ。もう行かないと思います。 | 17 | 1 | 0 |
| 雰囲気が良くてゆったりできました。 | 17 | 1 | 0 |
この出力では、レビュー文から文字数・単語数・感嘆符の数などの情報を取り出して、テキストを数値化する例を示しています。感情や強調の傾向を特徴量として活用できます。
集約系特徴量(カテゴリごとの統計量を集計する)
特徴量エンジニアリングの中でも、特に強力で応用範囲が広いのが集約系特徴量(集計特徴量)です。これは、あるカテゴリに対して平均や合計、件数などの統計情報を集めて新たな特徴量として加える手法です。
もとのデータをそのまま使うのではなく、「グループに着目して情報を要約する」ことで、モデルがより高度なパターンを学習できるようになります。とくに顧客や商品、地域などのID単位での傾向を捉えたいときに効果的です!
グループ統計量
グループ統計量とは、カテゴリごとに数値データをグループ化し、その中で平均・中央値・標準偏差・最大値・最小値・合計・件数などを計算する手法です。
たとえば、「顧客IDごとの購買金額の平均」や「店舗ごとの1日あたりの売上件数」などがこれにあたります。
| 顧客ID | 購入日 | 購入金額 | 顧客平均 | 顧客合計 | 顧客購入回数 |
|---|---|---|---|---|---|
| A001 | 2024-04-01 | 1200 | 900 | 2700 | 3 |
| A002 | 2024-04-01 | 1500 | 1550 | 3100 | 2 |
| A001 | 2024-04-10 | 800 | 900 | 2700 | 3 |
| A003 | 2024-04-11 | 2000 | 2000 | 2000 | 1 |
| A002 | 2024-04-15 | 1600 | 1550 | 3100 | 2 |
| A001 | 2024-04-20 | 700 | 900 | 2700 | 3 |
この出力では、顧客IDごとに平均購入金額・合計金額・購入回数といった統計量を計算し、各取引データに付加することで、顧客全体の傾向を表す特徴量を作成しています。
このような集計値は、単なる一回の取引の情報だけでは見えない傾向を可視化するのに非常に役立ちます。たとえば、ある顧客が普段どのくらいの金額を使っているかがわかれば、異常値やハイパフォーマンス顧客の検出にもつながります。
カウントエンコーディング(出現回数の特徴量)
カウントエンコーディングは、あるカテゴリが何回出現したかを数えて数値に置き換える手法です。
たとえば、「Aという商品が10回登場している」「Bは3回だけ」などといった、カテゴリの頻度をそのまま特徴量にすることができます。
| 商品名 | 商品出現回数 |
|---|---|
| りんご | 3 |
| バナナ | 3 |
| りんご | 3 |
| みかん | 2 |
| バナナ | 3 |
| バナナ | 3 |
| りんご | 3 |
| みかん | 2 |
この出力では、「商品名」の出現回数をカウントし、それを特徴量として追加しています。その商品がどれくらいよく出てくるか(人気の高さ)をモデルに伝えるためのシンプルで効果的な方法です。
このようにこの方法はとてもシンプルですが、商品の人気度や顧客の来店頻度などを表現するのに非常に有効です。特に、カテゴリ数が多すぎて one-hot エンコーディングが使いにくい場合にも、軽量な代替手段として重宝されます!
ランキング系特徴量
ランキング系特徴量とは、カテゴリ内での順位を表すものです。たとえば、「同じ日付の中で売上が高い順に商品を並べて順位をつける」といった操作が該当します。
このようにして得られる順位情報は、売上トップの商品か、それとも下位の商品かなど、相対的な立ち位置をモデルに伝えることができます。
| 日付 | 商品名 | 売上金額 | 売上順位 |
|---|---|---|---|
| 2024-04-01 | りんご | 500 | 2 |
| 2024-04-01 | バナナ | 800 | 1 |
| 2024-04-01 | みかん | 300 | 3 |
| 2024-04-02 | りんご | 700 | 1 |
| 2024-04-02 | バナナ | 600 | 2 |
この出力では、同じ日付内で売上金額に基づいて商品に順位をつけることで、モデルに「その日の中でどれだけ売れたか」という相対的な立ち位置を伝えるランキング系特徴量を作成しています。
このように、順位を使うと、実際の数値そのものよりも「他と比べてどのくらいか」という視点での学習が可能になるため、特にスケールの大きいデータや分布が偏ったデータに対して効果的です!
特徴量選択
機械学習モデルにとって、「どんな特徴量を使うか」は予測精度に大きく関わる重要なポイントです。データに含まれるすべての特徴量を使えばよいと思いがちですが、実際には不要な特徴量を減らすことで、モデルがシンプルになり、精度や汎化性能が向上することがよくあります。
このように、有用な特徴量だけを選び出す作業を特徴量選択(Feature Selection)と呼びます。ここでは、代表的な3つの手法について、簡単に紹介します!
分散の小さい特徴量の除去
まず最も基本的な方法が、分散の小さい特徴量を除外する手法です。
分散とは、値のばらつき具合のことです。ある特徴量がすべてのデータでほとんど同じ値を持っている場合、それはモデルにとってほとんど何の区別ももたらさない無意味な情報であることが多いです。
たとえば、99%が「男性」で1%が「女性」のような極端な偏りがある場合、その特徴量はモデルを混乱させたり、逆に過学習を起こす可能性もあります。このような特徴量は、あらかじめ削除することで、モデルの効率と精度を改善できます。
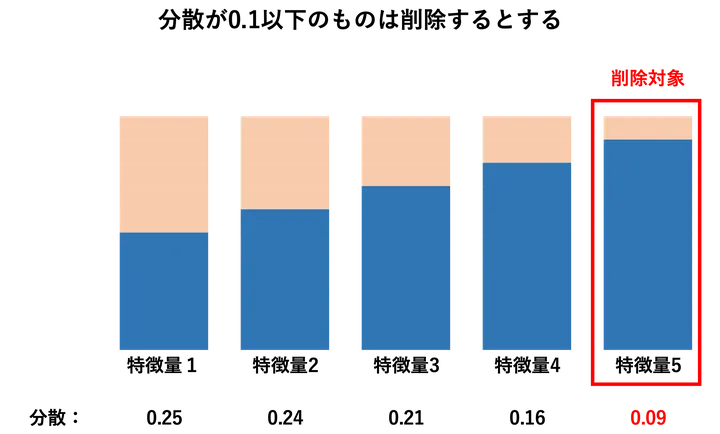
F値による特徴量の除外
F値は、各特徴量と目的変数との関係の強さを表す統計指標の一つです。回帰や分類の種類に応じて、適切なF統計量を用いて、特徴量がどれだけ目的変数と関連しているかを評価します。
簡単に言えば、「この特徴量は目的変数にどれくらい影響していそうか?」を数値でスコア化してくれるものです。例えば分類問題の場合、F 検定によって、カテゴリごとに各特徴量の平均値の違い(群間分散)を見て、その違いが偶然かどうかを評価します。目的変数が「購入した人」と「購入しなかった人」だった場合、それぞれで「年齢」の平均の違いが有意に異なるかどうかについて、F値を算出します。この違いが有意なら、年齢は目的変数と関連があると判断され、F値が高くなります。
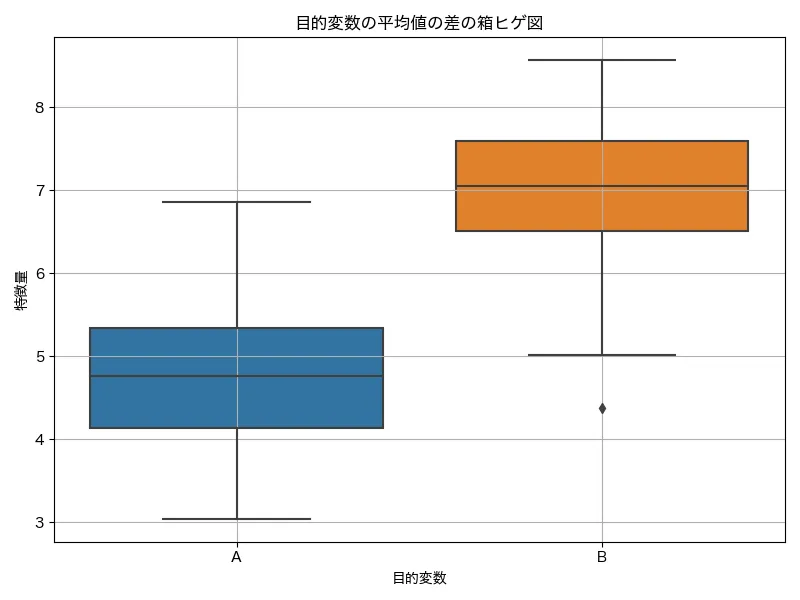
①2つのグループの平均を差を出し
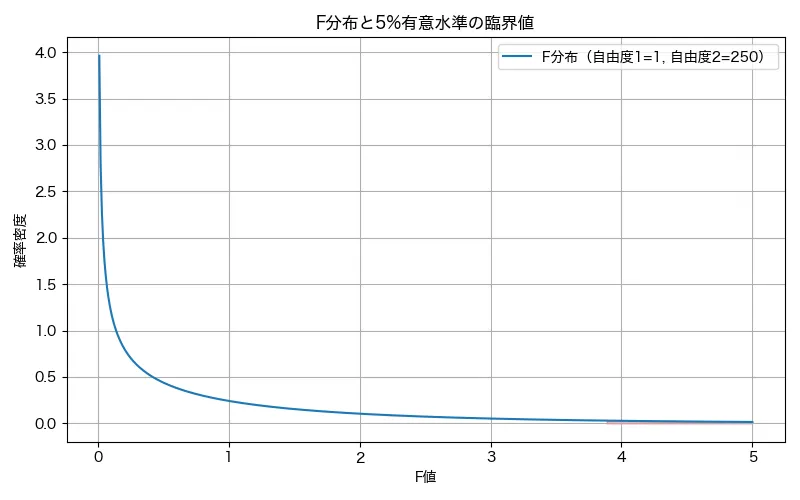
②その差の大きさをF値で統計的に評価
F値が小さい特徴量は、目的変数との関係が弱いと判断され、スコアの低い順に除外することで、重要な特徴量だけを残すという選択ができます。とくにデータが多く、手動では特徴量を評価できない場合に役立ちます!
モデルベースの特徴量選択
モデルベースの特徴量選択は、機械学習モデル自体を使って、どの特徴量が重要かを判断する手法です。
たとえば、決定木系のモデル(ランダムフォレストやLightGBMなど)は、特徴量の「重要度(feature importance)」を自動で計算してくれます。これにより、「モデルが予測に最も使っている特徴量」がどれかを可視化することができます。
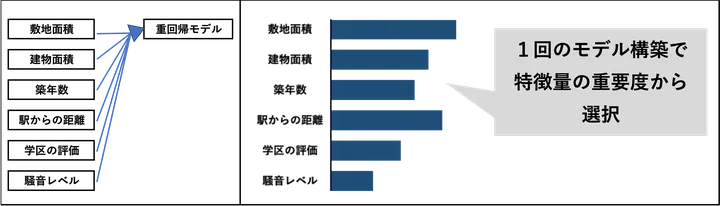
この方法の良いところは、実際のモデルの構造に即した重要度が得られる点です。ただし、モデルの種類によっては、重要度の計算方法が異なったり、解釈が難しくなることもあるため注意が必要です。
特徴量選択についてはいかに詳しく解説してあるので、よかったら参考にしてください。

まとめ
以上、特徴量エンジニアリグについての概要でした。ここで紹介した内容はどれも僕自身が実務で使っている手法で、予測精度を上げるためにとても大切なテクニックになります。ぜひ、参考にしてください!
