(※シリーズ「AI入門」は、筆者が、2023年・2024年に愛知県中小企業診断協会の理論政策更新研修での登壇内容「AIを活用した中小企業診断」の補足資料として、本サイトに掲載しています)
みなさんこんにちは、デジタルボーイです。
本シリーズ「AI入門」の第5回となる記事となります。今回はAI技術の中心とも言える「(伝統的な)機械学習」について、概要をお伝えしたいと思います。

デジタルボーイです。
データサイエンス歴20年以上のおっさんです。中小企業診断士として、データサイエンス、WEBマーケティング、SEOに関するデータ分析、コンサルティングの仕事をしています。自己紹介の詳細はコチラ
機械学習の基本概念:機械学習とは何か?
機械学習(maschine learning)とは、プログラムにデータを与えて、そのデータからパターンを見つけ出し、そのパターンを使って、パターン分類や予測やグループ分けなどを行う技術のことです。タイトルには機械学習の前に(伝統的な)という文言をつけています。伝統的な機械学習というのは、ここではディープラーニング以外の機械学習を指すことにします。
機械学習を理解する上で、重要な概念があるので、簡単に紹介します。
1. 特徴量と目的変数
特徴量というのは、AIに学習させるためのデータのことです。
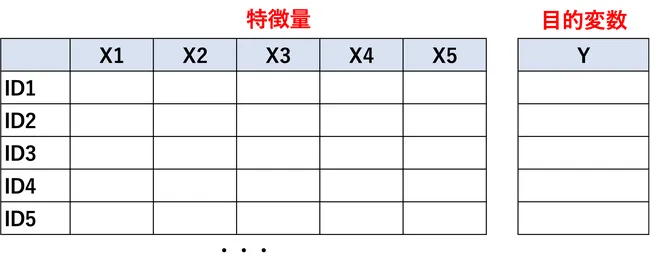
よく、学習塾のCMなんかで、「過去10年分の試験データをAIに食わせ、今年出題される試験問題を予測した」とか言うことがありますよね。この場合、特徴量は「過去10年分の試験データ」にあたります。
AIが学習するためのデータですね!AIはデータを学習することで、予測だったり、分類だったり、クラスタリングだったりを行います。逆にいうと、特徴量となるデータがないと、AIは学習できません。
もう一つのデータとして、目的変数というのがあります。目的変数というのは、AIが予測するためのデータのことです。さっきの学習塾のAIの例で言うと、「今年出題される試験問題」が目的変数にあたります。
学習塾の例
- 特徴量:過去10年分の試験データ
- 目的変数:今年出題される試験問題
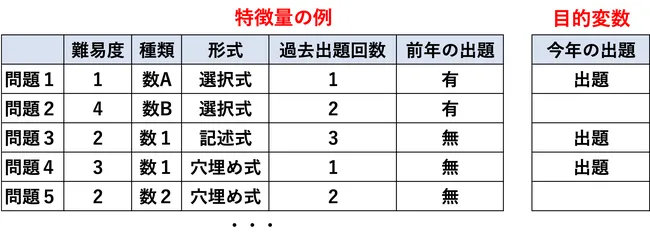
ここからわかるように、AIというのは特徴量を学習して、目的変数を予測するというのが、典型的なケースです。ちなみに、あとで解説しますが、目的変数がAIというもの存在します。
2. モデル
先ほど、特徴量と目的変数について説明しましたが、特徴量と目的変数を使って、AIに学習させるための仕組みがモデルです。
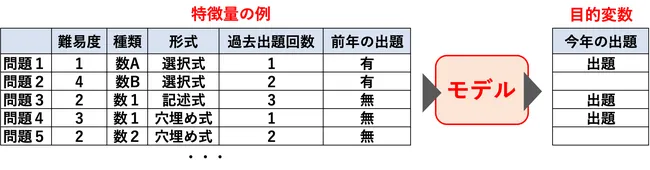
予測モデルでは、基本的に特徴量は過去のデータであり、手元にあるデータです。目的変数は、未来のデータであり、予測したいデータであり、手元にないデータです。手元にあるデータから、手元にない、未知のデータを予測するために、どうするのか?
ここで、AIモデルが登場します。例として、ある商品の売上数予測をする場合を考えてみましょう。
特徴量は、商品の価格、来店客数、広告費、曜日などで、目的変数は、当日1日の売上数とします。このように、手元にある特徴量でどうにか、未来の売上数を予測するために、AIモデルを使うんですね!
AIモデルは、大量で複雑な、特徴量の一定のパターンから予測値を出力します。
3. 教師あり学習と教師なし学習
教師あり学習というのは、特徴量(入力データ)と、目的変数(出力データ)を使って、モデルを学習させる方法です。教師というのは目的変数のことだと思ってください。
例えば、ある商品の売上数予測する場合、特徴量は、商品の価格、来店客数、広告費、当日の天気などで、目的変数は、売上数となります。売上数という目的変数を、AI技術を使って特徴量をモデル化するということですね!典型的な応用例としては、何かの予測だったり、分類だったり、が教師あり学習に該当します。
一方で、教師なし学習というのは、特徴量だけを使って、モデルを学習させる方法です。目的変数がないモデルのことになります。例えば、デパートで顧客を、顧客の購買パターンをもとに、AIを使ってセグメンテーションしたいとします。
この場合、特徴量は、顧客のいつ、どこで、何を、どのくらい買ったかといった購買履歴データだったり、顧客の性別・年齢・住所などの顧客属性などにあたります。
教師あり学習と異なり、このような場合は、明確に教示となるデータ(目的変数)がなく、いい感じにAIがデータからパターンを見つけ出し、セグメンテーションを行うことになります。
機械学習のモデルについて
ここでは、数ある機械学習のモデルの中でも基礎的なモデルについて、概要を紹介してみますね。
決定木
決定木は、以下の図のように、特徴量を組み合わせることで、目的変数を判定するための、ツリー構造のモデルです。
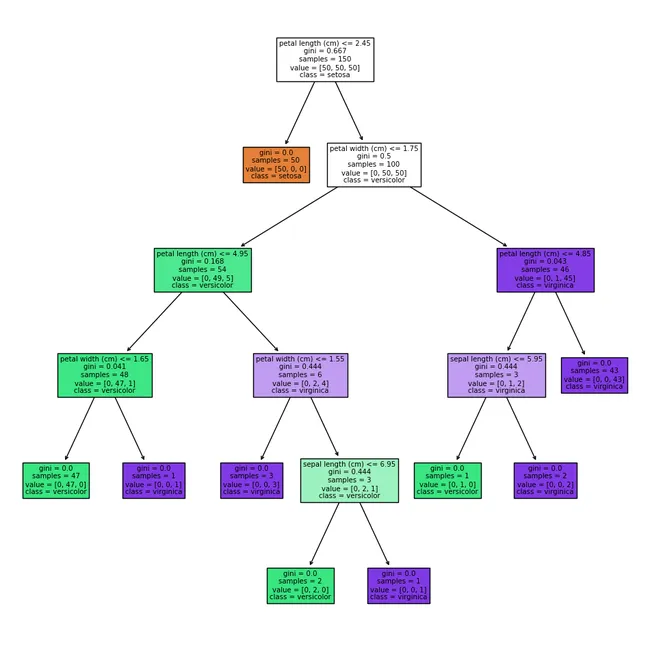
あみだクジのような形状をしていますね。実際のデータの分岐に沿って、あみだクジを辿っていくようにて、最終的な目的変数にたどり着きます。決定木は上の図のようなツリー図を出力することもあり、他の機械学習モデルと比べて、その判断過程が直観的に理解しやすいのが特徴です。
そのため、僕の場合は分析コンサルとしてお客さんに分析結果を提出する際の一発目としては、この決定木を使うことが多いです。お客さんも、あみだクジを楽しむ感じで、分析結果を理解してもらえるので、とても好評です。
ただし、決定木はそれ単体ではそれほど、他のモデルに比べて高い予測性能を持っているわけではありません。そのため、予測精度を高める必要がある場合は、決定木をベースにしてた、より高度な機械学習モデル(アンサンブル学習の手法であるランダムフォレストや勾配ブースティング)などを使うことがおおいです。
実用場面では、決定木は予測モデルの構築のためによく使われます。応用例としては、来店予測モデル、需要予測モデル、価格予測モデルなどの予測モデルですね。
回帰分析(線形回帰分析)
以下のように、入力(特徴量)と出力(目的変数)の関係性を数式で表現したモデルです。
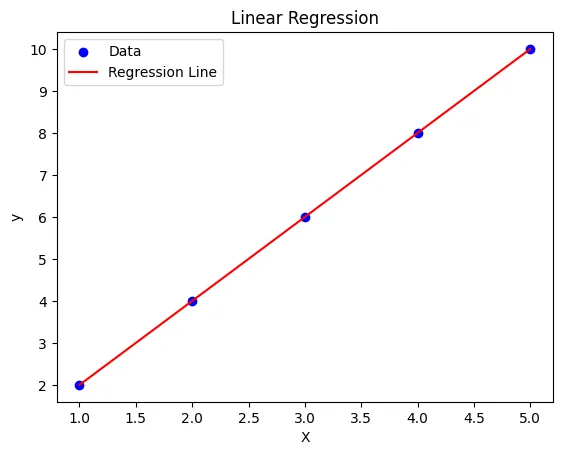
最も単純な形式が、下の図のような特徴量1変数、目的変数1変数の1対1の関係を示した線形回帰です。線形回帰は、特徴量と目的変数の関係が直線(比例関係)で表現できると仮定したモデルです。
例えば、商品の価格(特徴量)と売上数(目的変数)の関係が、ある直線上に乗っているとしましょう。この直線の傾きと切片を数式化したのが線形回帰モデルです。
y = ax + b
中学生の時に習った、直線の傾きと切片の式ですね!
このような直線を引くことで、何がいいのかというと、新しい未知のデータ特徴量が来たら、この数式に当てはめることで、目的変数の予測値を出すことができるところです。
とは言え、線形回帰は、データの関係性が単純な場合に適したモデルであり、現実のデータは複雑で非線形な場合も多いため、いろいろなモデルを検討しながら、モデルを構築していく必要があります。
また、回帰分析の応用例については、決定木と同様、売上予測、需要予測、価格予測など、数値の予測タスクに広く活用されています。
ロジスティック回帰分析
ロジスティック回帰は、上の線形回帰分析の特殊なモデルです。
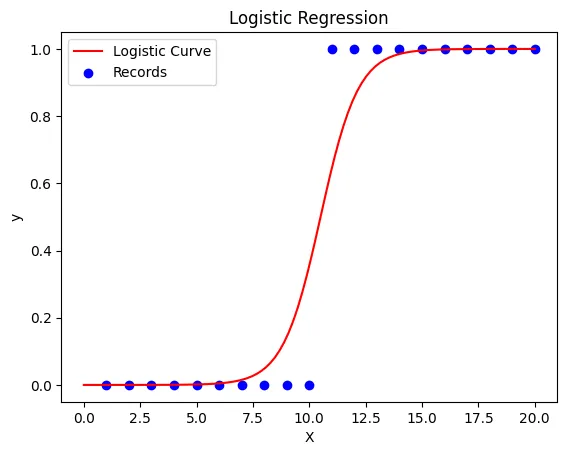
特徴量と目的変数の関係を線で表すという点では線形回帰と同様です。ただし、線形回帰分析との違いは、特徴量と目的変数の関係を直線ではなく、曲線で表しており、また、目的変数は連続的な値ではなく、0か1とか、true/falseなどの二値の判断をするモデルです。
例えば、ある人の年齢、収入、性別などの特徴から、その人が商品を購入するか(1)しないか(0)を予測するような問題に使えます。ロジスティック回帰のしくみについて、ごくごく簡単に解説してみます。
入力データ(特徴量)と目的変数(購買の有無)の関係を数式化すると仮定しましょう。
その数式は、先ほどの図のような、S字カーブの形をしています。このS字カーブの形を表す関数がロジスティック関数といいます。入力データを代入すると、0から1の間の数値(購買確率)が出力されます。この確率が一定の閾値を超えれば、購買ありと判断し、そうでなければ購買なしと判断します。
なので、ロジスティック回帰は、特徴量から予測値(確率)を出力し、その確率に基づいて2値の判断をする、というモデルになっているのがポイントなんですね!線形回帰が数値予測に向いているのに対し、ロジスティック回帰は分類問題に向いているといえます。
クレジットカードの不正利用検出や、メール配信の配信可否判断などでよく使われています。
k-means クラスタリング
わかりました。k-meansクラスタリングについても、同じように初心者向けに解説させていただきます。
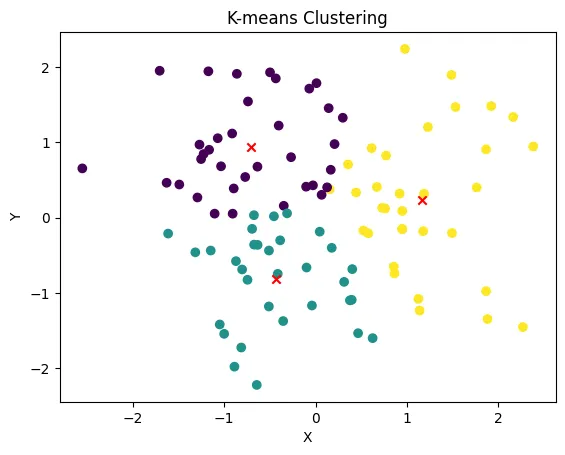
k-meansクラスタリングは、データを自動的にグループ分けするための手法です。上のモデル達と最も違う点は、このモデルは目的変数がないという点です。目的変数がないモデルというのはどういうことなのでしょうか?
上のモデル達は、主に予測や分類のめに使うモデルであり、手元のデータから、未知の目的となるデータを予測したり、分類したりするために使われます。
それに対して、このk-meansクラスタリングなどの、目的変数がないモデルは、データ自体の性質を活かして、データをグループ分けするために使われます。では、簡単に、モデルの仕組みについてみていきましょう。
まずは、データを何個かのグループ(クラスタ)に分けたいと考えます。そのクラスタの数を、あらかじめkと決めておきます(k-meansの「k」の由来です)。
次に、各クラスタの中心点(平均値)を、とりあえず初期値として適当に設定します。
図のように、そして、各データがどのクラスタの中心点に一番近いかを計算し、そのクラスタに割り当てていきます。すると、クラスタごとにデータが集まってきます。そこで、クラスタの中心点を再計算し直します。
このプロセスを、中心点の位置が安定するまで繰り返していきます。
最終的には、データが k個のクラスタに自動的に分けられあがります。データ間の自然なグループ分けが行えるのがk-meansの特徴です。
例えば、顧客の購買データから、k-meansクラスタリングを使って、顧客の似たようなグループを見つけ出すことができます。それによって、効果的な販促施策の立案などにつなげられます。
このように、k-meansは教師データがなくても、データ自体の性質を活かしてグループ分けできるのが魅力の1つです。直感的に理解しやすいクラスタリング手法として知られています。
まとめ
以上、古典的な機械学習の説明でした。古典的機械学種とひとくくりにしましたが、ここで扱っていないモデルもじつは沢山の種類があります。すべてのモデルについて精通するのは難しいですし、現実的ではありません。そのため、業務で使うモデルはどんなものなのかという観点で、調べてみて、
より使う頻度の高いモデルを重点的に学習するといいのではないでしょうか。
次のコラム

前のコラム


