みなさん、こんにちは。デジタルボーイです。
今回はデータ分析で利用される統計や統計的手法について解説したいと思います。

デジタルボーイです。
データサイエンス歴20年以上のおっさんです。中小企業診断士として、データサイエンス、WEBマーケティング、SEOに関するデータ分析、コンサルティングの仕事をしています。自己紹介の詳細はコチラ
データ分析と統計分析の違いって?
データ分析の手法の多くは統計分析の手法に基づいています。
さらに、データ分析の理論的な発展や理論的な正確性についても統計的な理論が基礎となっています。
そのため、データ分析を学術的に研究しようとした場合、統計学の研究は必要不可欠なのですが、では、現実場面では「統計学の知識がなければ、データ分析ができないか」というと、そういうわけでもありません。
例えば、自動車は、エンジンを動力源とした機構を持った4輪の乗り物ですが、自動車の動力機構を理解しなければ自動車の運転ができないかというと、そうでは無いですよね。もちろん、自動車の内部の構造や仕組みを理解していれば、自分で整備や修理も可能です。そのため、自動車の構造について詳しく理解しておくことが、自動車を保有する上で無駄になるというわけでもありません。自動車を運転するために、自動車の構造を理解することはアドバンテージになるが、かといって必ずしも必要というわけでもない、といったところでしょう。
このような関係が、データ分析と統計学の知識と言えるでしょう。
データ分析をする上で、統計学の知識がたくさんあった方が良いに越したことはありませんが、なくてもどうにかなるというのが実情では無いでしょうか。
それにも関わらず、「車乗るんやったら、オイル交換とかタイヤ交換くらい、ひとりできんなアカン!」「車はマニュアルに限るヤロ、オートマなんか車ちゃうわ!」とか、車に対してやたらこだわりの強いおっさんも中にはいます。同じように、データ分析の世界にもやたら数学とか統計学にこだわりの強いおっさんも中にはいます。まあ、そんなおっさんに出会ったとしても、心の中で「やかましいわ、チー牛!!そんなんやから、会社でも、その年で今だに平社員なんじゃ、ボケ!」とひとしきり悪態をつき、基本的には無視してしまいましょう。一方で、そんなおっさんがあなたの会社の上司だったら、とりあえず転職エージェントに登録してみるのもいいでしょう。データサイエンティストは現在売り手市場ですし、転職のしやすい職種だと思います。
とはいえ、転職を考える前に、データ分析を理解する上で必要最低限の統計学の知識を理解することは、間違いではないでしょう。ここでは、データ分析に必要最低限の統計の知識について解説したいと思います(数式は最低限の解説ですし、僕は決して統計学にこだわりの強い人間でもないので、決して僕に対して、暴言は吐かないように)。
データ分析のやり方についての初歩的な点については、こちらに解説記事を書いていますので、よかったら見てみてください。

データ分析で知っておきたい、統計の基本知識「記述統計」
統計学の世界には「記述統計」という理論があります。これは、手元のデータの特徴を数値で表すための指標(統計量と言う)です。要約統計量と言ったりもします。
ここではデータ分析をする上で、ぜひ、知っておきたい基本的な記述統計量についてピックアップしてみます。念のため、数式を書いていますが、わからない場合は数式だけ読み飛ばしてください。
また、以下のグラフはPythonというデータサイエンスが可能なプログラミング言語で書いています。データサイエンスのツールについては以下に記事を書いていますので、よかったら見てみてください。

データの中心を要約するための統計量
平均値(Mean):皆さんご存知のいわゆる平均です。手元データの全ての値の平均です。
対象データの合計をデータ数で割ることで算出します。
$$ \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i \ $$
中央値(Median): 手元データを半分に分けた時の値です。
最頻値(Mode): 手元データで最も件数の多い値です。
データが整数で、左右対称の分布の場合、概ね、平均値・中央値・最頻値は分布の真ん中で一致します(下図左参照)。
一方、歪んだ分布の場合、平均値・中央値・最頻値は一致しません(下図右参照)。
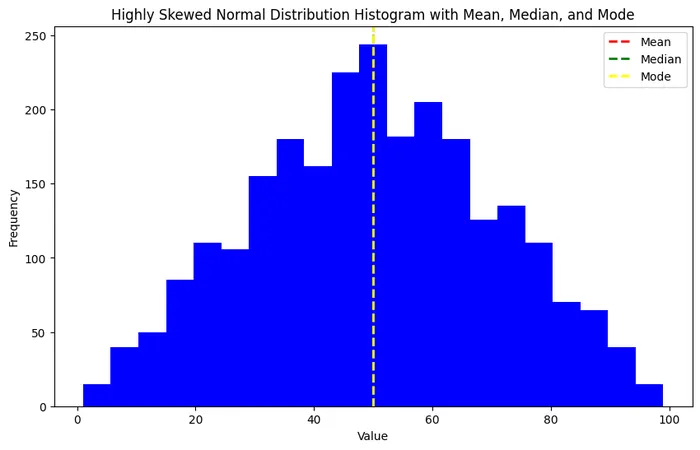
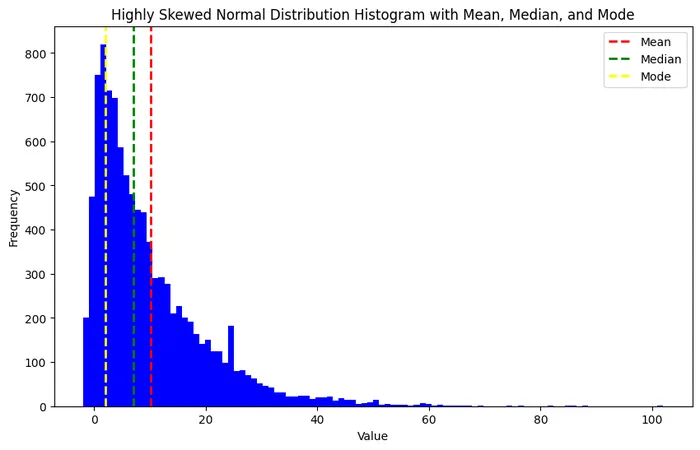
図:平均・中央値・最頻値が一致する分布と、一致しない分布の例
日常、私たちは「平均値」と言われると、なんとなくその分布の真ん中の値を想像すると思います。しかし、2つのグラフを見てもらうとわかると思いますが、平均値と言っても分布の真ん中に位置する場合もあれば、端っこに位置する場合もあります。平均値が分布のどの辺に位置しているのかについては、データ分析を進める上で実は非常に重要なポイントになることがよくあります。
一つ例を挙げますね。2013年花巻東高校の卒業生の平均年収は、なんと4,000万円!!と言われています。これは、東京大学卒業生の平均年収を超えているとのことです。このことだけを聞くと、自分の子供はなんとしてでも花巻東高校に入れたい!と思うかもしれませんが、実はカラクリがあります。これは大谷翔平選手がドジャースで10年約1,000億円の契約を結んだことに起因しています。大谷選手が一人で、年収の平均を押し上げているからなんですね。実際のデータの分布ではありませんが、イメージとしては以下のような分布となります。
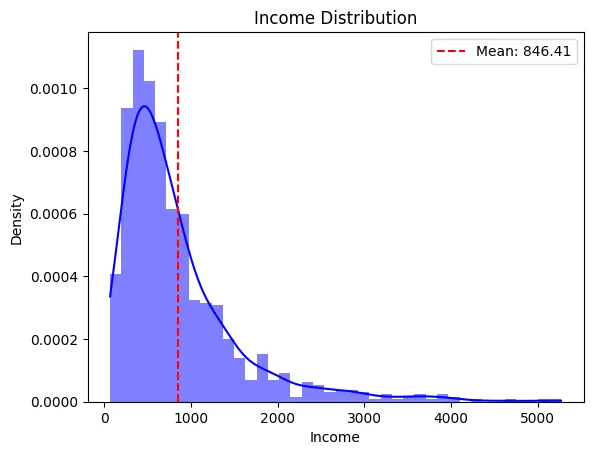
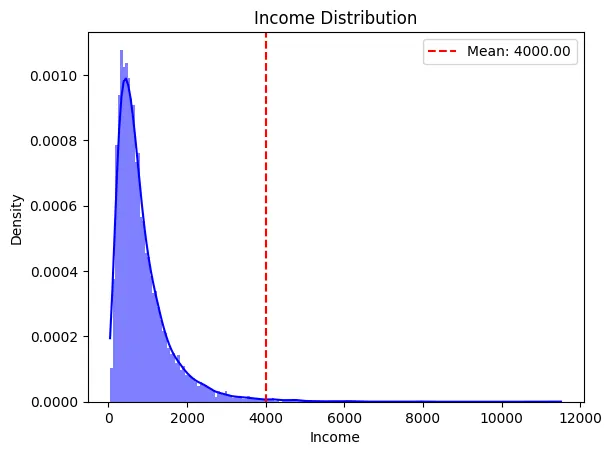
図:年収分布と平均値(赤線)の分布のイメージ。
左が通常の分布、右が大谷選手一人で平均を押し上げているイメージ
ここからも平均値だけでデータの全貌を理解したつもりになるのは、非常に危険であることがわかると思います。
そのため、分析するデータは常に左右非対称であるとは限らないため、データの分布をグラフ化し、平均値・中央値・最頻値を確認することをお勧めします。
データのバラツキを要約するための統計量
分散(Variance): 手元データの分布が平均値からどれだけ散らばっているか
を示す指標です。
言葉で表すと「平均からの偏差の2乗の平均」
$$ \sigma^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i – \bar{x})^2 $$
標準偏差(Standard Deviation): 分散の平方根で計算します。
$$ \sigma = \sqrt {\frac{1}{n} \sum (x_i – \bar{x})^2} $$
偏差値:標準偏差から計算する指標
$$ 偏差値 = 50 + 10 \times \frac{(得点 – 平均値)}{ 標準偏差 } $$
標準偏差も偏差値も分散から計算される統計量です。偏差値は受験生の中における自分の相対的な位置を知るための指標としてよく使われますね。
以下のグラフは分散が1の分布と2の分布(正規分布)を同時にプロットした図になります。
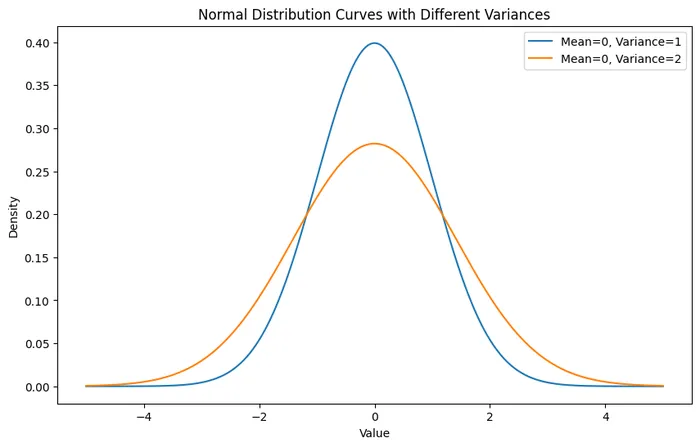
図:同じ平均で分散が異なる二つの分布の例
分散が大きい分布は、バラツキも大きく、横に広がった分布であることがわかると思います。
2つのデータ間の関係を表す統計量:相関係数
身長と体重や、国語の点数と英語の点数など、2つのデータ間の関係を表す指標に相関係数という統計量があります。
相関係数は次のような性質があります。
- 相関係数は-1から+1の間の値を取ります。
- 相関係数の符号(正または負)は、二つの変数間の関係の方向を示します。
相関係数の符合がプラスの場合、正の相関関係があると言います。
一方の変数が増加するともう一方も線形に増加します。
逆に相関係数の符合がマイナスの場合、負の相関関係があると言い、一方が増加するともう一方が線形に減少います。 - 相関係数の絶対値は、関係の強度を示します。絶対値が大きいほど、関係は強く、小さいほど弱くなります。
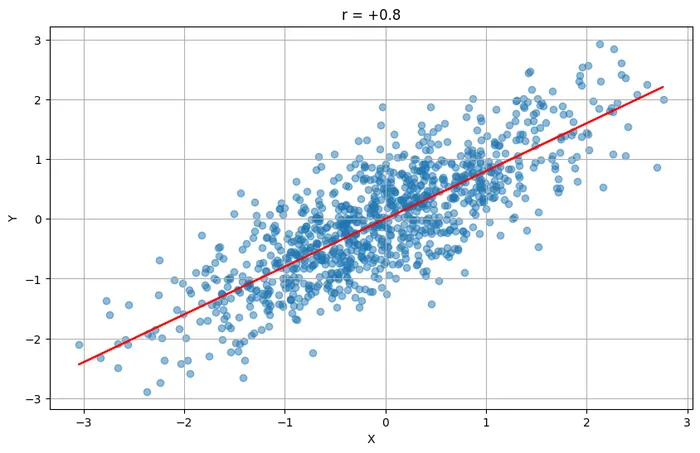
ちなみに、相関係数で測れる2つの変数間の関係は、正確には、2つの変数間の直線的な関係といいます。
例えば、2つの変数間に曲線的だけれども強い関係があった場合も、相関係数は曲線的な関係を図ることはできません。
この辺の相関係数については、次の記事でも詳しく解説しますので、よかったら見てくださいね

さらにデータ分析を勉強する上で知っておきたい統計の知識「多変量解析」
データ分析の勉強を進めていくと、より高度な統計的手法として多変量解析という手法を勉強する機会があるでしょう。
多変量解析は複雑に絡み合ったデータを統計的な手法を用いて、解明するための手法です。
次が代表的な多変量解析の手法になります。
主成分分析:
多次元のデータの次元を削減し、データ間の関係を抽出するための手法。
例えば、短距離走のタイム、長距離走のタイム、投てきの距離、ダンスの上手さ、などの運動に関する多次元のデータから、<瞬発力・持久力>というように、運動能力を2次元の合成変数で数値化することが可能です。
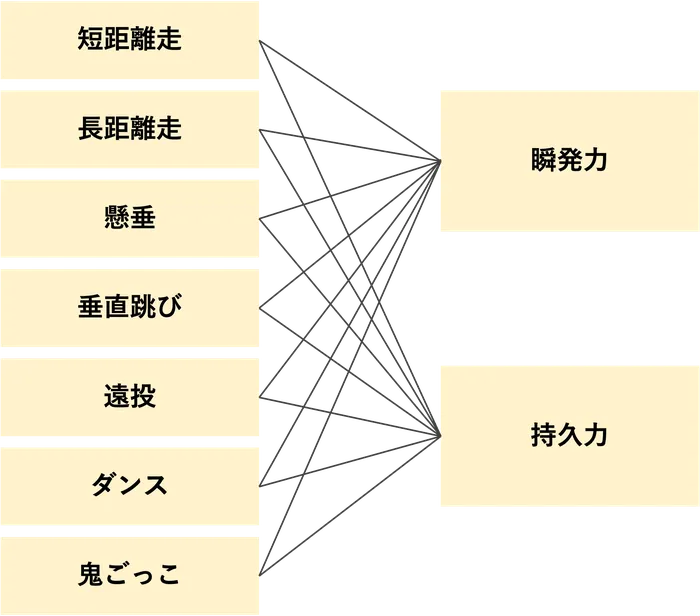
図:主成分分析の観測変数と合成変数の関係の例
因子分析
心理学で発展した手法で、観測変数の背後にある潜在的な変数(潜在変数/因子)を抽出するための手法。
例えば、アンケート項目から、ストレス因子の抽出など、物理的に測定できない概念を数値化することが可能です。手法的には主成分分析と非常によく似ている分析手法ですが、考え方として、主成分分析が複数の変数から合成変数を算出する考えに対して、因子分析は、潜在変数(原因)から変数(結果)が観測されるという考え方をし、図の矢印も主成分分析と異なり、因子を丸で描き、矢印も潜在変数から観測変数への方向で表現されます。
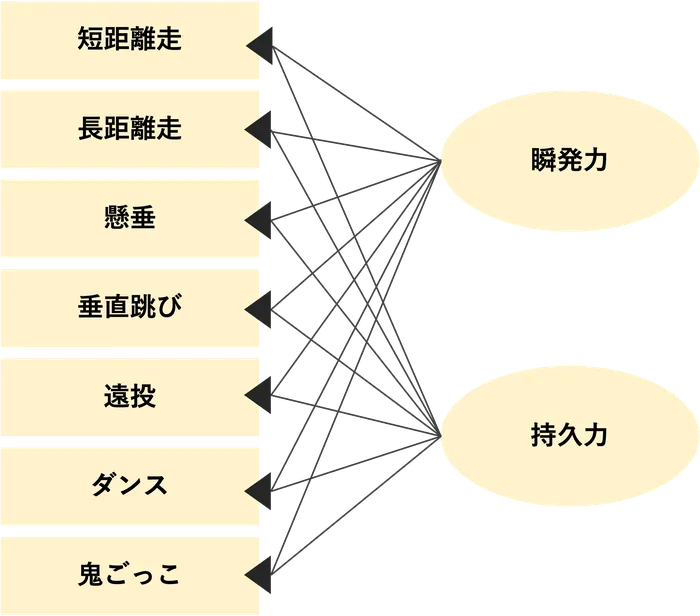
図:因子分分析の観測変数と合成変数の関係の例
クラスタ分析
似たような特徴を持つデータをグループ化するための手法。
例えば、ECサイトのユーザーに対して、健康志向クラスタ、ブランド志向クラスタ、知的好奇心志向クラスタ・・・など
顧客クラスタのグループ化が可能
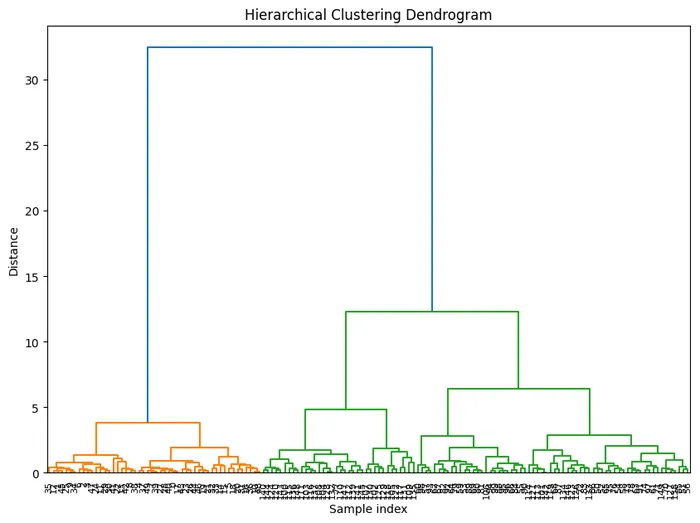
図:クラスター分析の樹形図(デンドログラム)
回帰分析
複数の予測変数を用いて、目的となるデータを予測するための手法。
例えば、気温、湿度、天気から、明日の遊園地の入場人数を予測することが可能です。
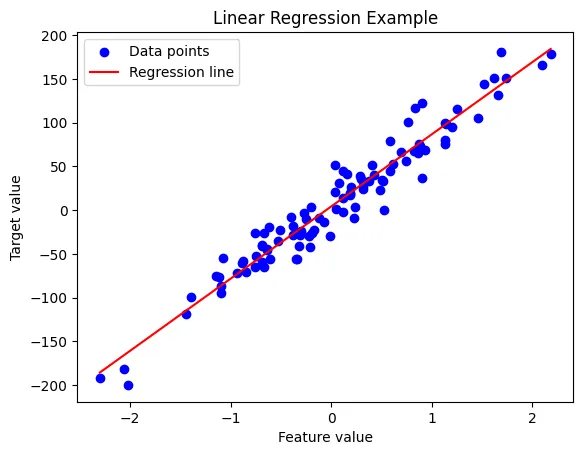
図:回帰分析
ロジスティック回帰分析
データの傾向から、特定のカテゴリを分類するための手法。
例えば、製品の長さ、硬さ、色などから、不良品と正常品を分類することが可能です。
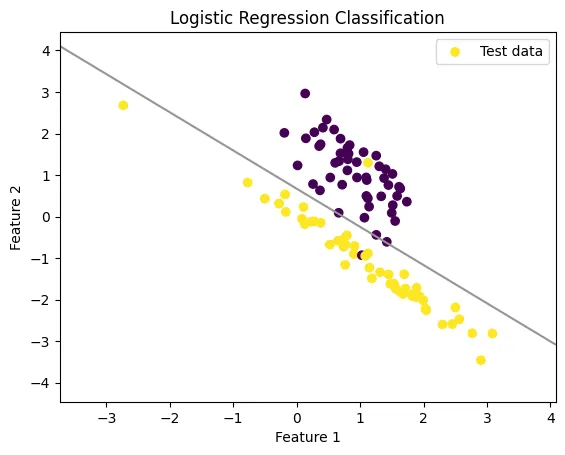
図:ロジスティック回帰分析
これら多変量解析を用いることで、人の力では分析が困難な多次元で構成される複雑なデータをわかりやすく数値化、ビジュアル化し、傾向を分析することが可能です。
ここら辺の分析方法で「何を選ぶか」については、分析の方針によって色々変わってきます。分析の方針についてはさらにいかにも記事を書いていますので、よかったら見てみてください。

以上が、データ分析に関連する統計的手法の解説になります。
実は統計がわからなくても、AIを使って分析もできる!
以上は伝統的な統計についての超初歩的な解説です。ここら辺はデータサイエンティストだったら知っておいて損はない内容です。とはいえ、このような統計についても知らなくても、実は最近はデータ分析できたりもします。それが「AIを使ったデータ分析」なんですね!
なかなか、便利な世の中になってきました。AIを使った分析のざっくりとした流れは、以下のとおりです。
AI(機械学習)が可能なツールでデータを読み込み、
AIが読み込めるようにデータを加工し、
AIモデル(機械学習モデル)を構築し、
AIモデル(機械学習モデル)を検証し、
構築したモデルを運用化、アプリ化する
という流れになります。
AIについての分析についてはこちらにも解説してありますので、よかったら見てみてください。

まとめ
データ分析の学習を進めていくと、これら統計的手法に遭遇すると思います。
そして、これらの数理的な背景は、高度な統計理論から成り立っており、書籍によっては、難しい数式が多く出てくることもあると思います。
しかし、そのような数式も、自動車の内部構造と同じで、興味のある人は学習すればいいですし、興味がなければ、すっ飛ばして、ソフトウェアで実際に分析する技術を中心に学べばそれで十分、現実場面ではやっていけます。
ちなみに、統計学に必要な数学など、データ分析に関するおすすめ書籍はこちらにも記事に書いていますので、よかったら、みてください。

いずれにしても、あまり数式には気を使わずに、データ分析の学習を進めていってくださいね。
その他、データ分析については以下に記事をまとめています。よかったらみてください!


