シリーズ「データ分析入門」第７回：データ分析におけるデータの集計

みなさん、こんにちは、デジタルボーイです。
今回は、データ分析におけるデータの集計について解説したいと思います。

記事を書いた人

デジタルボーイです。
データサイエンス歴20年以上のおっさんです。中小企業診断士として、データサイエンス、WEBマーケティング、SEOに関するデータ分析、コンサルティングの仕事をしています。自己紹介の詳細はコチラ

データ分析とデータの集計の違いは？

データの分析と集計については、特に学術的に定義があるわけではありません。
そのため、厳密に、「これはデータ分析だ」とか「これはデータの集計だ」と言い切れるものでもないので、その点を念頭に解説したいと思います。

多くの場合、データ分析というプロジェクトの中の一つの作業としてデータの集計があります。例えば、アンケートデータの分析プロジェクトを例にとって見ていきましょう。

1. 企画
2. 仮説立案
3. アンケート項目の作成
4. アンケートの実施
5. データの集計
6. データの分析
7. 結論

概ね、このような作業の流れで進めると思います。

この内、狭義の集計作業は５の「データの集計」となります。

僕の感覚では、ここでのデータの集計作業は、アンケートデータの入力作業や件数の集計、性別・年齢・居住エリアなどのフェイス項目の集計、アンケート項目ごと平均の集計、自由記述のまとめ・・・などある程度、機械作業や単純作業で可能なデータの取りまとめ作業を指しますね。

一方、狭義のデータ分析作業は、６の「データの分析」となります。僕の感覚では、立てた仮説が正しいのかデータを分析することが当てはまり、あるアンケート項目に対して、男女別で違いはないか？とか、年齢によって違いはないか？など、仮説に対してそれをデータ分析を行いながら検証していくような作業を指します。

そのため、ざっくりとですが、以下のようなイメージでいいのではないでしょうか

データの集計：仮説に基づかずに機械的にするデータの取りまとめ作業。データ分析の前作業
データの分析：仮説に基づき、データを深掘りし検証する知的作業

ということで、以降では、データの集計に焦点を絞って解説したいと思います！

データの集計にはどんな種類がある？

データの集計の方法は大きくは次のような手法に分けられます。

• 単純集計
• クロス集計
• グラフ化・ビジュアライズ
• 相関

それぞれの手法について見ていきましょう。

単純集計

一つのデータに対して、集計を行うことを単純集計と言います。以下はアンケート結果と単純集計の例となります。

単純集計結果は以下の通りです。

例：アンケート結果の単純集計の例

上記の例では複数選択が不可のため合計値は１００％でしたが、もし、複数選択が可能なアンケートの場合の合計値は１００％を超えます。

また、以下のような、順位で回答させるアンケート項目の場合は次のような集計になります。

単純集計結果は次の通りです。

例：順位によるアンケート結果の単純集計の例

上の図では1位と挙げた人数の各項目の構成比を出しているため、縦方向で結果を足すと合計が100となっています。一方、各項目内（「データ分析の手法について」等）での構成比を出した場合は縦方向で結果を足しても100になりません。

1位に挙げている項目が知りたい場合は縦方向の構成比である前者の集計方法で、項目内の順位の構成比が知りたい場合は横方向の構成比である後者の集計方法となります。この点も、どのような集計が必要なのかについて考えながら集計をする必要がありますね。

クロス集計

単純集計の後は、クロス集計についてです。

先ほどの単純集計は１つのデータに対して集計を行う手法でした。クロス集計は２つ（２つ以上）のデータに対して行う集計です。

例で見ていきましょう。

例：アンケート項目「あなたがデータ分析業務で使うプログラミング言語は何種類ありますか？」

について、年齢別のクロス集計結果は次の通りです。

このように、縦と横で２つのデータをクロス集計表で表します。
ちなみに、表中の、上側を表頭といい、左側を表側という場合もあります。

クロス集計では、単純集計で扱わなかった２つ（以上）のデータを同時に集計するため格段に集計結果としての情報量が増えました。

このようにクロス集計では、集計結果としての情報量が増えた一方で、気をつけなければならないポイントもあります。

最低限気をつけていただきたい３つのポイントについてお伝えしたいと思います。

クロス集計で気をつけなければならないポイント１：
縦と横の、どちらの軸で集計をするか？

上のプログラミング言語の数と年齢のクロス表について、同様のデータで、次のように表現した物をご覧ください。

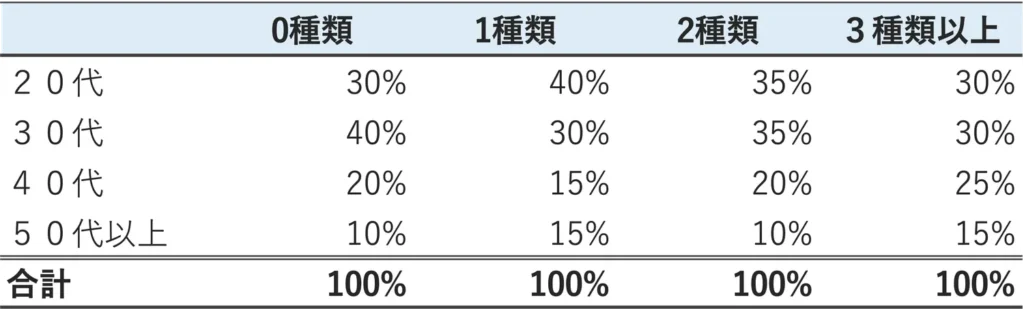
図：同じデータで集計の方法の異なる２つのクロス表

両者の違いはわかるでしょうか？

同じクロス表ですが、上側は横軸で構成比を取っており横軸の合計が１００％になっており、下側は縦軸で構成比を取っており、縦軸の合計が１００％になっています。

一見するとどちらも意味のあるクロス集計表ですが、下のクロス集計表はほとんど意味のない集計表です。ほとんど意味のないという理由は次のとおりです。

下の集計表ではデータ分析業務で使うプログラミング言語の種類を「０種類」と答えた人を抜粋しましょう。

• ２０代・・・　　３０％
• ３０代・・・　　４０％
• ４０代・・・　　２０％
• ５０代以上・・・１０％

以上のように、合計が１００％という集計です。

もし、このアンケートでは、年代別の回答者数が同じになるように、回答者を選んでいたのであれば、この構成比も意味があります。しかし、通常のアンケートでは、年代ごとに回答者数はバラバラです。例えば、ネットアンケートであれば、若年層の回答者が多くなるでしょうし、有料セミナーなどでアンケートを取れば、より年齢の高い層の回答者が多くなるでしょう。

上の表の「０種類」と回答した年代は３０代が最も多いという結果ですが、そもそも３０代の回答者数が多いアンケートであった場合、その結果は、単純に３０代の回答者数の構成比を色濃く反映しただけの結果でしかありません。

このようなこともあるため、クロス集計表の構成比を出したい場合は、どの縦と横の軸でどちらの軸を100%と置いて集計すべきかについて、十分注意して集計するようにしましょう。

クロス集計で気をつけなければならないポイント２：
グルーピングできなか？

アンケート項目でよくある＜嫌い・少し嫌い・普通・少し好き・好き・＞
といった５段階の項目（専門用語では「５件法」と言います）ごとのクロス集計は
次のような形式になります。

以下は質問結果です。

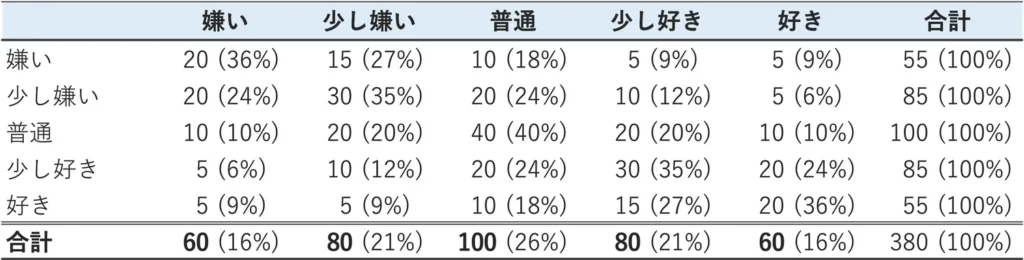
図：質問１と質問２のクロス集計表

上の表は５×５のクロス表のため、２５のセルがあります。このようなセルの多いクロス表をもとに、傾向を読み取る作業ははなかなか難しい場合が多いです。

このような場合には、「嫌い」と「少し嫌い」を嫌いグループ、「好き」「少し好き」を好きグループと言うように、思い切って項目をまとめることで、分析がしやすくなる場合があります。さらに図のように件数の多いセルの色を変えることで、よりわかりやすいクロス集計表ができました。

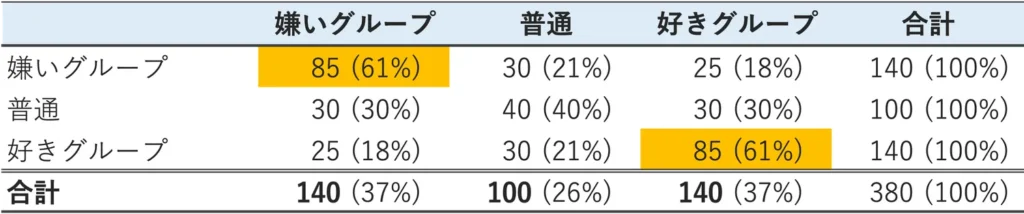
図：５×５のクロス表を、３×３の見やすいクロス表にする

この結果から、データ分析に携わる人にとって、統計学の勉強が好きな人はプログラミングの勉強も好きな傾向があり、
逆に統計学の勉強が嫌いな人はプログラミングの勉強も嫌いな傾向がある、との傾向が見られました。

クロス集計で気をつけなければならないポイント３：
その他の要因の影響はないか？

次の例です。ある会社の営業部門では、年間の契約数が１０件を超えた営業担当者に対して、特別賞を付与しています。

そこで、それまでの受賞歴の集計を男女別に行ったところ、以下のような結果でした。

図：男女別に見た、特別賞受賞者の集計

この表から、特別賞を受賞したことのある営業担当者は女性で39％、男性で59％でした。

この結果から、この会社の経営陣は「我が社では男性社員の方が特別賞を受賞した割合が高い。そのため、男性の方が優秀であると結論づけられた。今後は男性の営業マンをもっと採用しよう！」と結論づけました。

しかしです！

この結果にどうしても納得のいかなかったのが、この会社の新進気鋭のデータサイエンティスト、出井田 才艶子（でいた・さいえんす）さんです！

新進気鋭のデータサイエンティスト、出井田 才艶子（でいた・さいえんす）さん

彼女は「営業成績の良し悪しは、男女の差ではなく、勤続年数によって違うのではないか？」という仮説を立て、先ほどと同じデータから、さらに２つのクロス集計を出し、反論しました。

図：勤続5年未満の社員に絞った、男女別の受賞歴の集計表

図：勤続5年以上の社員に絞った、男女別の受賞歴の集計表

このクロス集計表は初めのクロス集計と同じデータですが、さらに勤続5年未満の社員（上表）と5年以上の社員（下表）の２つのパターンに場合分けした表です。

上の表から勤続5年未満の社員では、男性も女性も受賞ありは２０％と同様の比率であることがわかります。下の表から勤続5年以上の社員では、受賞ありの比率は女性で６０％、男性で５７％と若干女性の方が受賞ありの比率は高いくらいでした。

このような結果はなぜ起こったのでしょうか？

実は、営業成績の良し悪しを分ける本来の要因は「勤続年数」であり、勤続年数が長くなるにつれ営業経験が増し、成績は向上するのでした。一方、この会社では男性の方が勤続年数の長く、女性の方が勤続年数が短い傾向がありました。そのため、「男女差」でクロス集計表を作ったところ、男女で勤続年数に違いがあるために、勤続年数の影響が、男女差を通じて営業の良し悪しに現れたのでした。

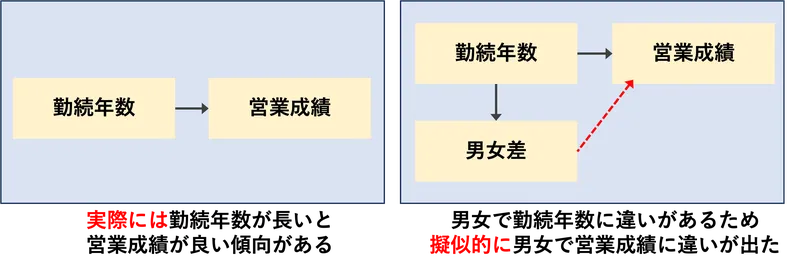
ここから、データサイエンティストは出井田 才艶子さんは

「営業成績の良し悪しは、男女差ではなく、勤続年数の差である。また、女性の方が勤続年数が低いため、今後は女性が長く働ける会社づくりをすることが、必要である」

と結論づけました。

この例のように、クロス集計表では、本来の要因が、他のデータの背後に隠れたために、関係のない他のデータがあたかも、違いの要因であるかのような結果が出る場合があります。

このようなことがあるため、単に機械的にクロス集計表を作るのではなく、「２つのデータの背後に、本来の要因となるデータがあるのではないか？」ということを注意深く検討しながら、集計を進める必要があります。

グラフ化・ビジュアライズ

続いて、グラフ化やビジュアライズについて見ていきましょう。数値をグラフにする理由はいくつかありますが、主に次の３つでしょう。

• プレゼンテーション等で数値をわかりやすく見せるため
• データに外れ値(極端に離れた一部の値)や異常値がないかを探るため
• データ全体の傾向を把握するため

グラフには以下のようなものがあります。

棒グラフ

棒グラフの例

グラフと言えば、まず思い浮かべる物ですね。応用範囲も非常に高いグラフです。まずは、棒グラフで集計できないか、を考えてみるといいでしょう。

折れ線グラフ

折れ線グラフの例

時系列のデータを表現するグラフです。人によっては、時系列データでないデータを折れ線グラフで表す人もいますが、基本的には時系列データは折れ線グラフ、そうでないカテゴリカルなデータは棒グラフと言うように棲み分けるといいでしょう

円グラフ

円グラフの例

構成比の集計を表すためのグラフです。項目が多くなったり、比率の小さな項目は潰れてしまうので、そのような場合は、「その他」の項目でグルーピングして表現しましょう。

帯グラフ

帯グラフの例

円グラフと棒グラフの特性を持ったグラフですね。一つ一つの棒が構成比を表しており、構成比の比較をするためのグラフです。クロス集計表をグラフ化する際にもよく使われます。

アンケートデータの集計でもよく使うグラフですね

ヒストグラム

ヒストグラムの例

一見棒グラフに見えますね。ある区間に該当する件数を集計したグラフです。年齢分布や収入分布など、分布を表したい場合によく使われるグラフです。

箱ひげ図

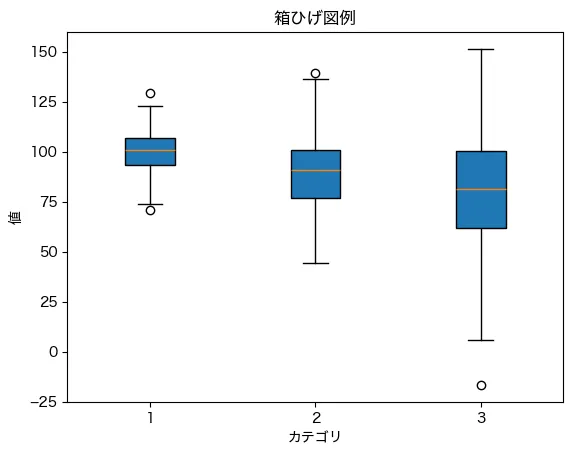
箱ひげ図

あまり見なれなグラフですね。

箱の中央の線は中央値（メディアン）を表しています。

また、箱の上下の端は第1四分位数（Q1、データの下から25%の地点）と第3四分位数（Q3、上から25%の地点）を示しています。

箱の上下に伸びた線は「ひげ」と呼ばれ、Q1とQ3から1.5倍のIQR（四分位範囲）の範囲内にある最大値と最小値までを示します。

この範囲外にある値は外れ値とみなされ、通常は丸や点でプロットされます。ビッグデータなどのデータに対して、データの振る舞いや概要をざっと見渡したい場合に、この図を使います。

僕自身はExcelによる利用よりも、PythonやRで大規模データの集計を行う際にデータの概要をつかむ際、よく使います。

レーダーチャート

レーダーチャートの例

個人の能力やゲームのキャラクターの能力を調べる際のグラフによく使われます。

僕自身は、企業の経営診断やコンサルを行う際、ある企業の売上総利益率、営業利益率、自己資本比率、固定比率、流動比率などの経営指標をレーダーチャートで示し、企業の評価をする際に、よく使います。

相関と散布図

２つの変数の関係性を集計しグラフ化する際には、次の散布図が非常によく使われます。

散布図の例

例えば、国語の得点を横軸、と数学の得点を縦軸などでグラフ化します。

また、相関係数という統計量も散布図と一緒に使われる指標です（正確にはピアソンの相関係数）。この相関係数は−１から＋１までの範囲をとります。

以下はそれぞれの相関係数が+0.8、+0.4、0、−0.4、−0.8の５つのパターンで作った散布図の例です。

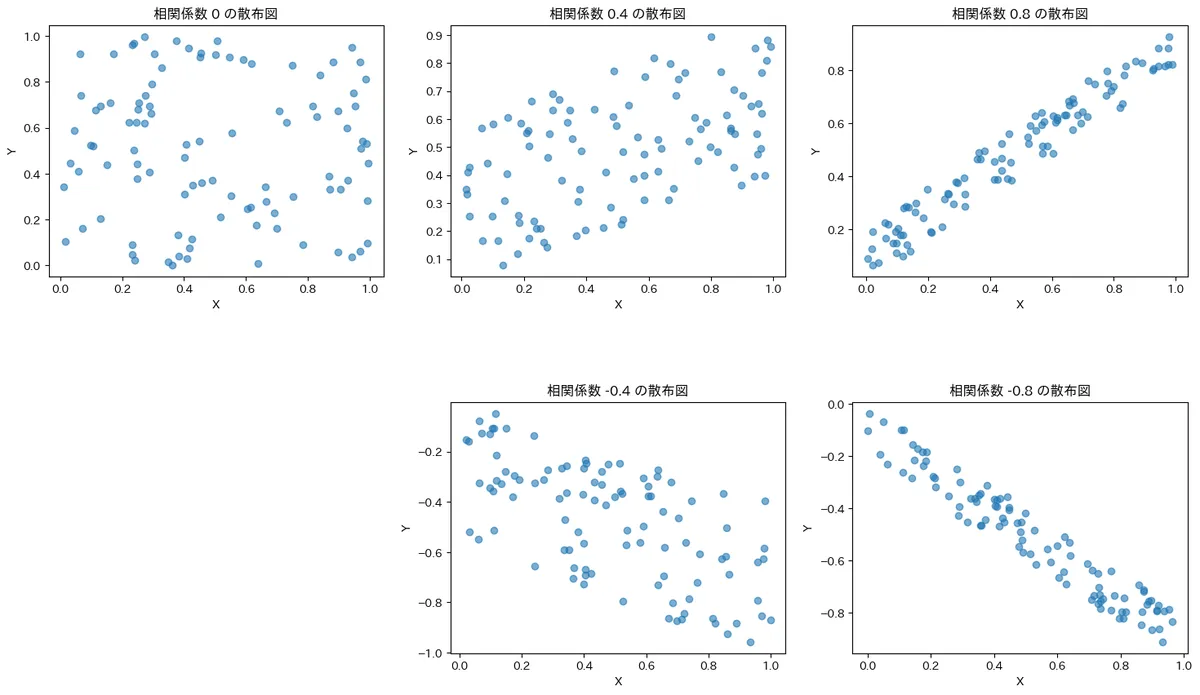
様々なパターンの相関係数で作った散布図の例

相関係数はグラフを見るとわかるように、次のような性質が見られます。

• ＋の場合は比例関係、ーの場合は反比例の関係
• 数値（絶対値）が大きいほど直線的な関係が強い
• 数値（絶対値）が小さいほど直線的な関係が弱い

ちなみに、この「直線的な」という表現は相関係数を表す上で非常に重要です。例えば、２つのデータ間の関係が非常に強くとも、直線的な関係が弱い場合は相関係数は０に近くなるからです。

次の例は、２つのデータ間に曲線的に非常に強い関係がある場合の散布図です。

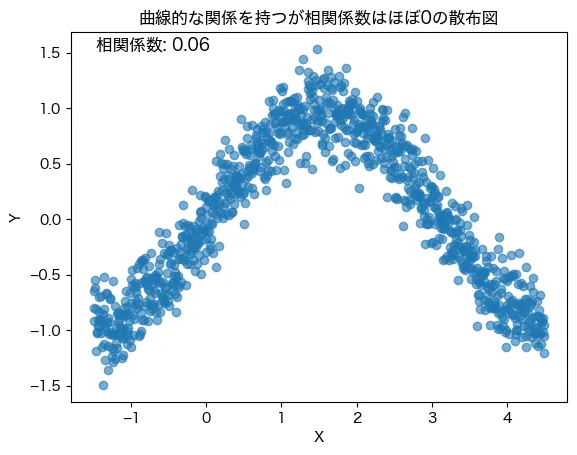
図：曲線的な強い関係があるが、相関係数は０のケース

一見してわかる通り、 X軸が左に行くほどY軸の値は下がり、同様にX軸が右に行くほどY軸の値も下がり、X軸の中心が最もY軸が高くなっています。明らかに、XとYで（曲線的な）強い関係がありそうですよね。

例えば、普段の運動量がXで、健康の指数がY軸だった場合、全く運動しないもの運動しすぎるのも健康に悪く、ほどほどの運動が最も健康にいいといったような関係です。

しかし、このような曲線的な関係も相関係数を見ると0.06とほぼ関係はないと言えます。

このようなこともあるため、集計した数値だけでデータを判断するのではなく、グラフ化による集計結果の確認もデータ分析を行う上で、非常に重要であることがわかります。

データの集計をするためのツールには何がある？

データを集計する際のツールは以下のように考えるといいでしょう。

上の質問のように、プログラミングができる場合や勉強したいと思う場合は、PythonかRがおすすめです。２つとも高度なデータ分析が可能で、かつ複雑なデータの加工や集計も得意としています。

どちらがいいかについては好みによりますが、データ分析以外にプログラミングをやるつもりは無かったり、より手っ取り早く習得したい場合はRがいいでしょう。

逆に、アプリ開発などもやって見ないと思うなら、Pythonがおすすめです。

もし、プログラミングができない場合や、勉強もしたくないという場合は、AccessとExcelという選択肢になるでしょう。

特に1万件を超えるデータ件数や複数のファイル（テーブル）を結合したり参照しながらデータの加工や集計が必要な場合はAccessを選択すべきですね。Excelも1万件以上のデータが扱えないわけではないですが、動きが格段に悪くなります。

また、別テーブルの参照についてもExcelの場合、別シートへの参照することで、できないこともないのですが、これまた非常に動きが悪くなりストレスに感じます。また、Excelで集計や加工をした際、何か手順が間違ったり、データを差し替えた際、これまでの作業と同じことを繰り返す必要もあるため、作業量が膨大になります。

その点、プログラムができれば、一度作ったプログラムに対してデータを差し替えて再度、そのプログラムを流すということはよくありますし、Accessについてもある程度、データを差し替えて同じ作業を繰り返すということは可能です。

そのため、ある程度複雑な集計やデータ容量の大きな集計をする際は、Excel以外のツールの習得も視野に入れるといいでしょう。

データ分析ツールについてはこちらにも記事を書いています。よかったら見てくださいね

あわせて読みたい

シリーズ「データ分析入門」第８回：データ分析のためのおすすめツール5選 みなさん、こんにちは。デジタルボーイです。今回は、データ分析を行うために必須のツールについて解説したいと思います。これからデータ分析を始めたいという方にとっ…

まとめ

以上、データ分析における集計について解説して見ました。

集計というと、なんとなく、「データ分析が高度なもので、集計は低レベルなもの」というようなイメージを持たれることもあるかもしれませんが、実査にやってみると非常に奥の深い作業であることがわかると思います。

今回ご紹介した内容も、見るだけでなく実際にツールを使って実データで集計してみるとグッと理解が深まると思います。

ぜひ、チャレンジして見てくださいね！