こんにちは、デジタルボーイです。今回は特徴量選択の基本とPythonプログラミングについて解説したいと思います。

デジタルボーイです。
データサイエンス歴20年以上のおっさんです。中小企業診断士として、データサイエンス、WEBマーケティング、SEOに関するデータ分析、コンサルティングの仕事をしています。自己紹介の詳細はコチラ
特徴量選択について
僕がデータ分析を勉強し始めてはや20年、駆け出しのデータサイエンティストだった頃に比べ、現在はデータ分析基盤の発展もあり、データの「ビッグデータ化」はめちゃめちゃ進行しているように思います。ただ、残念なんですが分析データのビッグデータ化は進み、分析データの特徴量(説明変数)は爆発的に増加してきているんですが、それに対して、予測に使える意味のあるデータはそれほど増えていない印象です。
ビッグデータ化が進んで・・・
- 分析データの特徴量は爆発的に増えているが、
- 予測に使える意味のあるデータは、それほど増えていない
このような状況で、手元データを全てモデルに投入し、精度が上がれば良いですが、大量の特徴量がある場合それをモデルに投入することで精度が逆に下がったり、モデルがうまく学習できなかったりします。
そこで重要になってくるのが、特徴量選択(変数選択、feature-selection)になります。特徴量選択を用いることで、統計的に意味のある特徴量を事前に選択することで、意味のある特徴量に選別してモデルに投入することが可能となります。
今の時代のビッグデータへのデータサイエンスでは、ではなくてはならないテクニックといえますね!
ということで、今回は、前半に特徴量選択の考え方、後半にpythonによる特徴量選択の実践と実験を行いたいと思います!なお、今回ご紹介する特徴量選択手法は以下となります(全てpythonにて実行可能な手法)。
- 分散による特徴量削減
- 単変量統計検定に基づく特徴量削減
- モデルベースの特徴量選択
- 再帰的特徴量削減
- 逐次特徴量選択
では順を追って見ていきましょう!
お時間のない人のための、結論!!
今回の実験で、もっとも安定して精度の高い特徴量選択をするにはsklearnのSelectFromModelでランダムフォレストを指定するのが良かった。また、コツとして、threshold=-np.infを指定することが重要
from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import RandomForestRegressor
selector_model = SelectFromModel(
estimator=RandomForestRegressor(n_estimators=150, random_state=42),
max_features=150,
threshold=-np.inf
)また、速度を重視する際は決定木(DecisionTreeRegressor)を使うといい。
分散による特徴量削除について
分散による特徴量削除は、一定の分散を持たない特徴量を削除する方法です。具体的には、すべてのサンプルでほぼ同じ値しか取らない特徴量は情報量が少ないと判断し、削除する手法です。
この手法は主に、one-hotエンコーディング後のカテゴリカル変数や、0/1のブール値を多く含むデータなど、基本的にはカテゴリカル変数に対して使われるイメージです。例えば、「東京都に住んでいるか」のような列で、ほとんどのサンプルが0(= 都外)であるような場合、その列は分散が非常に小さくなり、除外の対象となります。
逆に、連続変数の数値データについては、通常分散が小さいからといって意味がないとはえず削除することはありません。
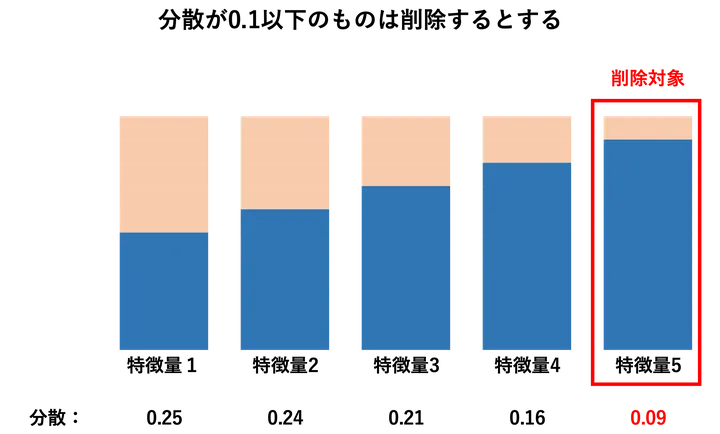
具体例
例えば、あるデータセットに0か1のみを取るブール値の特徴量(フラグ)があり、100件中1が10件、残り90件は0だったとします。
この場合、1の出現割合(確率)は10%です。ちなみに、このようなデータはベルヌーイ分布に従うとみなせるため、分散は以下の式で計算されます。
分散 = p × (1 – p)
ここで、p = 1の出現確率 = 10 / 100 = 0.1
したがって、
分散 = 0.1 × (1 – 0.1) = 0.1 × 0.9 = 0.09
この0.09という分散は比較的小さく、モデルにとって重要な情報をほとんど持っていない可能性があります。特に、他にも似たような特徴が多数ある場合は、こういった特徴を削除することで学習のノイズを減らし、モデルの精度や学習時間を改善することができます。
なので、このような特徴量を除外するには、しきい値を例えば 0.1 に設定すれば、この特徴量(分散 0.09)は削除されます。
メリット・デメリット
分散による削除は、非常に高速かつ直感的な手法で、特徴量数の多いデータにおける前処理として有効です。学習時間の削減や、不要なノイズの除去による精度の安定化に貢献します。また、教師あり・教師なしを問わず使える点も利点です。
ただし、1の出現頻度が極端に低くても、その1が分類上非常に重要な意味を持つケースもあります。例えば、極めて稀な病気の有無を示す特徴が予測精度に大きな影響を与える可能性もあるため、こうした場合は分散だけを根拠に削除しないよう注意が必要です。
単変量統計検定に基づく特徴量選択について
単変量統計検定に基づく特徴量選択は、特徴量を1つずつ取り出し、それぞれが目的変数とどれだけ関連しているかを統計的に検定し、関連性の高いものを選択します。一般的には分散分析などでも使われるF 検定のF値が、特徴量選択でもよく使われます。
分類の場合(目的変数がカテゴリ):F 検定によって、カテゴリごとに各特徴量の平均値の違い(群間分散)を見て、その違いが偶然かどうかを評価します。例えば、目的変数が「購入した人」と「購入しなかった人」だった場合、それぞれで「年齢」の平均の違いが有意に異なるかどうかについて、F値を算出します。この違いが有意なら、年齢は目的変数と関連があると判断され、F値が高くなります。
回帰の場合(目的変数が連続値):回帰モデルをあてはめたときに、その説明変数(特徴量)が目的変数の変動をどれだけ説明しているかを見る形でF検定によるF値が算出されます。一般的には、回帰係数の有意性検定と同じ構造となります。
算出したF値から選別:例えば、F値の上位10件を採用するとか、下位の20件は削除する、などというようにF値を基準に特徴量を取捨選択します。
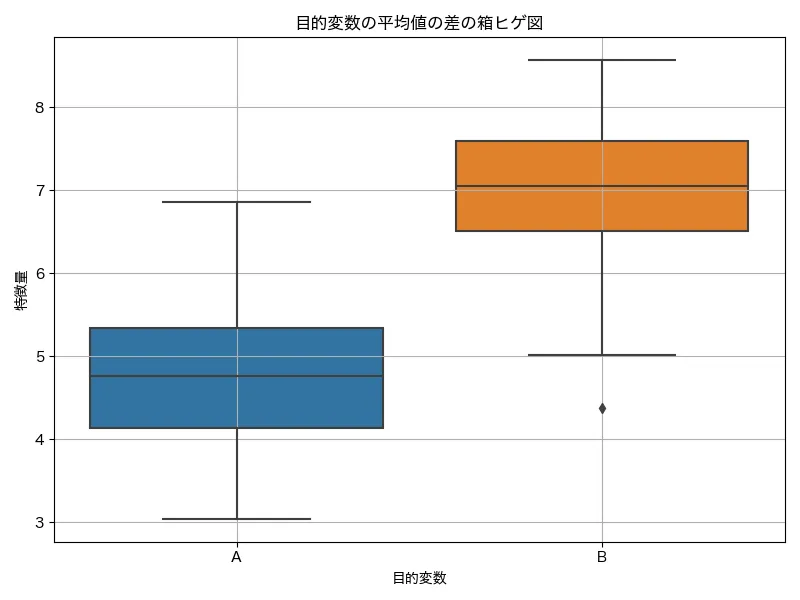
①2つのグループの平均を差を出し
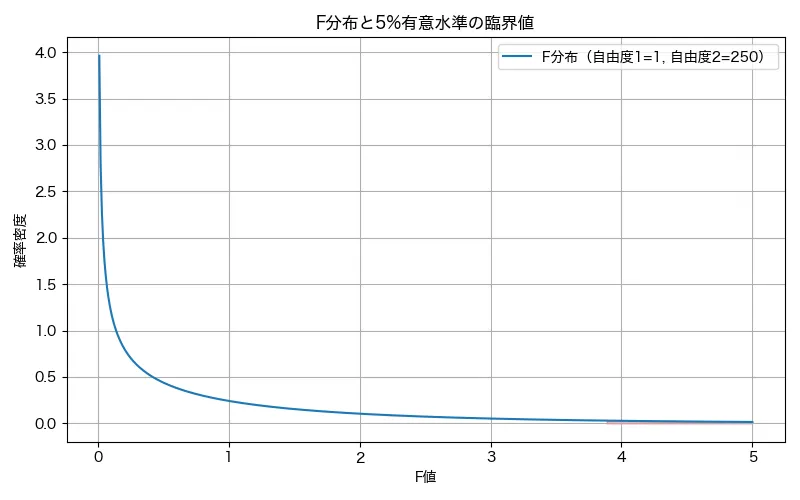
②その差の大きさをF値で統計的に評価
使用シーン
この手法は、特徴量の数が多く、それぞれが目的変数とどれだけ関係しているかを早期に見極めたい場面で有効です。データの前処理段階で、明らかに関係が薄い特徴量を排除することで、後続のモデリングの効率や精度を向上させることが期待できます。特に、目的変数との線形な関係や相関が重要となる場面で有効です。
メリット・デメリット
この方法の大きな利点は、簡単かつ高速に計算できることです。各特徴量を独立に評価するため、大量の特徴量がある場合でも比較的容易に処理できます。また、モデルに依存しないため、前処理としても使いやすいです。
一方で、すべての特徴量を単独で評価するため、特徴量間の組み合わせや相互作用を考慮することができません。以下に例を挙げてみますね。
交互作業が重要になる例:
ある健康診断データで、「年齢」と「運動習慣(する/しない)」という2つの特徴量があり、目的変数は「糖尿病の有無(あり/なし)」だったとします。
このとき、単変量だけで評価すると:
- 「年齢」単体では、若くても高齢でも糖尿病の有無に大きな差が見られない
- 「運動習慣」単体でも、それほど明確な関連性が見られない
という結果になるかもしれません。
しかし、「高齢かつ運動しない」人だけが明確に糖尿病の割合が高く、「若年かつ運動する」人は極めて少ない、という交互作用的な構造がある場合、年齢と運動習慣を掛け合わせた特徴(年齢 × 運動の有無)を用いることで、糖尿病の有無と強い相関が見えてきます。
このように、単変量の検定では見逃されやすい重要な特徴が、特徴量同士の組み合わせ(交互作用)として現れることがあるため、単変量手法だけに依存するのは危険であり、後続のモデルや別の選択手法で補う必要があります。
このような場合はモデルベースでの特徴量選択などを利用すると良いでしょう。
モデルベースの特徴量選択について
続いてモデルベースの特徴量選択です。この手法は学習済みモデルが出力する「特徴量の重要度」に基づいて、重要な特徴量だけを選び出す方法です。線形モデルであれば回帰係数、決定木やアンサンブルモデルであれば特徴量重要度などを利用して、どの特徴量が目的変数の予測にどれだけ寄与しているかを数値で評価します。一定のしきい値以上の重要度を持つ特徴量だけを残すことで、無関係な特徴量を除外し、モデルの精度向上や過学習の防止、計算コストの削減などを図ることができます。
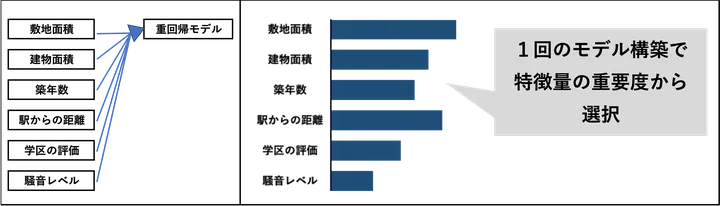
たとえば、住宅価格を予測するタスクにおいて、複数の数値的な特徴量(敷地面積、築年数、駅までの距離、周辺騒音レベルなど)を用意したとします。まずランダムフォレスト回帰モデルを学習させ、各特徴量の feature_importances_ を取得します。その後、重要度が一定値以上の特徴量だけを残すように設定し、それ以外の特徴量は削除します。これにより、価格にあまり影響を与えない特徴量(例えば「最寄りコンビニまでの距離」など)を除外し、より効率的かつ精度の高いモデルが得られます。また、Lasso回帰のようなL1正則化モデルでは、多くの係数が0になるため、0でない係数を持つ特徴量だけを残すといった選び方も可能です。こうした方法は SelectFromModel を使って簡単に実装できます。
逐次選択・再帰的選択と、モデルベースの特徴量選択の違い
例えば、逐次選択・再帰的選択・モデルベースによる選択で、重回帰モデルを活用した場合、どちらも「モデルを使って重要な特徴量を選ぶ」という点では共通していますが、選択の進め方と評価基準が異なります。
モデルベースの特徴量選択では、重回帰モデルを一度だけ学習し、そのときの回帰係数(coef_)をもとに、係数の絶対値が大きい特徴量だけを選びます。特徴量の重要度は、モデルに学習させた時点の係数で判断します。そのため、一度の学習結果を使って、すぐにに特徴量の選別ができる点が特徴です。例えばpythonのscikit-learnのモデルベースの特徴量選択のライブラリであるSelectFromModel を使うと、係数が0に近い、あるいはゼロの特徴量を機械的に除外できます。
一方で、再帰的特徴量削減(RFE)や逐次特徴量選択(SFS)は、何度もモデルを学習し直しながら、特徴量の組み合わせを探索していきます。RFEは重要度の低い特徴量を少しずつ削除していくのに対し、SFSはモデルの予測性能を基準に、特徴量を1つずつ追加または削除していきます。これらの手法では、「特徴量を1つ追加したらモデルのR²が上がったか?」みたいな感じで、実際のモデル性能の変化を見ながら選択を進める点が特徴です。
なので、モデルベースの選択は「一度の学習結果から重要度だけで選ぶ」方法であり、逐次選択や再帰的選択は「モデルの性能を実際に試しながら、より良い特徴量の組み合わせを探す」方法です。前者は高速で手軽ですが、後者のほうが精度や汎化性能において柔軟かつ実践的な選択ができる可能性があります。
メリットとデメリット
モデルベースの特徴量選択は、学習済みモデルが出力する特徴量の重要度を利用して、不要な特徴量を除外するシンプルかつ効率的な方法ですね!
最大のメリットは、モデルが一度学習されていれば、係数や重要度スコアをもとに機械的に特徴量を選べるため、処理が非常に高速かつ簡単である点です。特に、Lasso回帰やランダムフォレストのように、特徴量の重要度を自動的に計算してくれるモデルと相性が良く、スケーラブルなデータセットでも活用しやすい方法です。また、正則化によって自然に不要な特徴量の重みがゼロに近づくため、モデル自体が特徴量選択を内包しているケースもあります。
一方でデメリットとしては、一度の学習結果に完全に依存するため、特徴量間の相互作用や他の特徴との組み合わせによる影響を考慮できないという点があります。「重要度が低く見える特徴量でも、他の特徴との組み合わせで意味を持つ場合は見落とされるリスクがあります。この欠点は上で述べた「単変量統計検定に基づく特徴量選択について」のデメリットと同じです。また、モデルの種類によっては重要度の計算が安定しない場合もあり、モデルの選び方が結果に強く影響します。
したがって、モデルベースの選択は手軽で有効な一方で、「一度で終わる」ことの限界もあり、必要に応じて逐次的手法や交差検証と組み合わせて使うのが望ましい場面もあります。
再帰的特徴量削減について
ここで紹介する再帰的特徴量削減と次に紹介する逐次特徴量選択はモデルベースの特徴量選択法の発展型とも言えます。再帰的特徴量削減(Recursive Feature Elimination)は、重回帰モデルなどのモデルが出力する特徴量の重要度に基づいて、重要性の低い特徴量を少しずつ取り除いていく方法です。
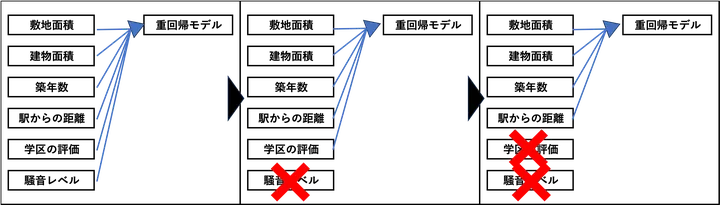
はじめにすべての特徴量を使ってモデルを学習し、重要度が最も低いものを削除します。その後、残った特徴量でもう一度モデルを学習し、同じように不要な特徴量を取り除いていきます。これを繰り返すことで、最終的に最も意味のある特徴量だけが残るようになります。
モデルベースの特徴量選択と再帰的・逐次特徴量選択の違い
- モデルベースの特徴量選択・・・モデルを一回だけ構築し、モデルが出力する結果(特徴量の重要度)から特徴量を選択する
- 再帰的特徴量削減・逐次特徴量選択・・・①モデルを構築→②モデルが出力する結果(特徴量の重要度)から1つの特徴量を選択/削減。①と②の処理をなん度も繰り返しながら1つずつ特徴量を選択していく
具体例
再帰的特徴量削減の仕組みを重回帰モデルで具体的に見てみましょう!
たとえば、住宅価格を予測するモデルを作るとします。手元のデータには、以下のような複数の説明変数(特徴量)が含まれていたとします。
- 敷地面積
- 建物面積
- 築年数
- 駅からの距離
- 学区の評判
- 周辺の騒音レベル
まずは、いったんこれらすべてを使ってまず重回帰モデルを学習させます。その結果、モデルが出力する回帰係数(重み)を確認すると、「周辺の騒音レベル」や「学区の評判」といった変数は、係数が非常に小さく、ほとんど住宅価格に影響を与えていなかったとします。次に、最も影響の小さい特徴量をひとつ取り除き、残った特徴量だけで再度モデルを学習させます。この手順を繰り返し、たとえば最終的に「3個だけ特徴量を残す」といった目標に到達するまで続けます。
使用シーン
この方法は、モデルが特徴量の重要度を数値として出力できる場合に有効です。たとえば、線形回帰や決定木のように、各特徴量の重みや重要度スコアが得られるモデルが向いています。どの特徴量を使うべきか判断がつかないときや、モデルの解釈性を高めたいときに役立ちます。また、最終的なモデルと整合性のある特徴量だけを残したい場合にも適しています。
メリット・デメリット
この方法のメリットは、モデルにとって本当に必要な特徴量を選び出せる点です。単純な統計的な検定とは異なり、特徴量どうしの関係性も加味しながら選択を進めていくので、モデルの精度向上にもつながる可能性があります。
一方で、何度もモデルを学習し直す必要があるため、計算に時間がかかるというデメリットもあります。特徴量の数やデータ量が多い場合は、かなりの時間がかかることもあります。また、選んだモデルの性質に結果が大きく左右されるため、使うモデルは慎重に選ぶ必要があります。可能であれば、交差検証などと組み合わせて使うと、より信頼性の高い特徴選択ができるでしょう。
逐次特徴量選択について
逐次特徴量選択(Sequential Feature Selection)は、特徴量を1つずつ追加または削除しながら、モデルの性能が最も良くなる組み合わせを探索する手法です。「前向き選択:forward」と「後ろ向き選択: backward」という2つのやり方があり、前向き選択では特徴量を1つずつ追加し、後ろ向き選択では全特徴量から1つずつ削除していきます。各ステップ毎回全ての特徴量を投入してみて最も良い性能を示す選択を採用していくことで、特徴量の組み合わせを最適化していきます。
ちなみに、この途中で切り上げずに全ての組み合わせを実施した後に最も良いものを採用する方法を、特徴量選択に限らず機械学習界隈では「貪欲法」(どんよくほう)と言います。
たとえば、10個の候補特徴量がある中から、最も予測性能が高くなる5個を選びたいとします。前向き選択では、まず1つの特徴量を使ってモデルを構築し、最も性能の良いものを1つ選びます。次に、残りの特徴量からもう1つ追加し、2つの特徴量でのモデル性能を評価します。この手順を繰り返し、5つ選び終えるまで続けます。後ろ向き選択の場合は、最初にすべての特徴量を使ってモデルを作成し、最も性能に影響を与えない特徴量を1つずつ削除していきます。
再帰的特徴量削減と逐次特徴量選択の違い
先述の再帰的特徴量削減(RFE)と逐次特徴量選択(SFS)は、どちらもモデルの性能を考慮しながら特徴量を選択していく手法ですが、特徴量の扱い方や選び方に違いがあります。
再帰的特徴量削減では、すべての特徴量を一度に投入しモデルを学習させ、その中で最も重要度の低い特徴量を削除します。そして、残った特徴量で再びモデルを学習し、また重要度の低いものを削除する、という操作を繰り返します。
一方、逐次特徴量選択は、モデルの性能を指標にしながら特徴量を1つずつ追加(または削除)していきます。前向き選択では、まず1つの特徴量でモデルを作成し、次に最も性能がよくなる特徴量を追加していく形で進みます。後ろ向き選択では、すべての特徴量から出発し、性能に最も影響が小さい特徴量を1つずつ削除していきます。特徴量の選択法は再帰的手法と異なり、特徴量の重要度ではなく、実際の予測性能の変化によって選択が行われます。
回帰モデルの例
再帰的特徴量削減・・・回帰係数(重み)の絶対値で特徴量を削除する
(前向き)逐次特徴量選択・・・モデルの性能(MSEや決定係数など)により特徴量を追加する
(後向き)逐次特徴量選択・・・モデルの性能(MSEや決定係数など)により特徴量を削除する
使用シーン
モデルの性能を維持または向上させつつ、不要な特徴量を減らしたいときに有効です。とくに、特徴量の数が中程度で、すべての組み合わせを試すのが現実的でない場合に適しています。また、他の特徴量選択手法と比較して、モデルの性能を直接指標にして選ばれるため、実運用に近い形で有用な特徴量を絞り込めます。
メリット・デメリット
メリットは、特徴量の組み合わせによるモデル性能を逐次的に評価しながら選択するため、単純な統計的な重要度やスコアだけでは判断できない、実際の予測力に基づいた特徴選択ができることです。また、複数の特徴量の相互作用をある程度考慮した選択が可能になります。
一方で、貪欲法であるため、初期の選択によって最終結果が大きく左右される可能性があります。最適解が保証されているわけではなく、あくまで準最適な特徴量セットにとどまることがあります。また、特徴量の数が多い場合には、すべての組み合わせを評価することが難しく、計算コストが高くなる点にも注意が必要です。
実データによる特徴量選択例とおすすめ使用法
これまで紹介した特徴量選択法について、実際の性能を実データをもとに実験してみましょう。実験については、python sklearnのfeature_selectionライブラリを使っています。データはsklearnのサンプルデータを使います。pythonコードについては後ろで記載しているので、良かったら自身のPCで実行してみてください!
特徴量選択で比較した手法と実験概要
今回は特徴量選択の手法と次の15種類で比較してみました。
比較した特徴量選択法
- 特徴量を全く削減しないベースラインモデル
- F値に基づく選択法:50個選択
- F値に基づく選択法:100個選択
- F値に基づく選択法:150個選択
- Lasso回帰を用いたモデルベースの選択法:50個選択
- Lasso回帰を用いたモデルベースの選択法:100個選択
- Lasso回帰を用いたモデルベースの選択法:150個選択
- 決定木を用いたモデルベースの選択法:50個選択
- 決定木を用いたモデルベースの選択法:100個選択
- 決定木を用いたモデルベースの選択法:150個選択
- ランダムフォレストを用いたモデルベースの選択法:50個選択
- ランダムフォレストを用いたモデルベースの選択法:100個選択
- ランダムフォレストを用いたモデルベースの選択法:150個選択
- 再帰的特徴量選択法(重回帰ベース)
- 前向き逐次特徴量選択法(重回帰ベース)
上記の選択法を使い、以下で紹介する1460件、9,290個の特徴量を持つデータに対して、予測モデルを構築しました。
構築した予測モデル
- 構築した予測モデル:重回帰モデル
- モデルの学習と検証:1460件中1022件をモデル学習に、438件を検証に実施し
- モデル評価:438件の検証データにおける決定係数R2 値で判断
実験の概要とデータの加工について
データの概要
実験用のデータは、scikit-learnから取得できる「House Prices」データセットを用いました。このデータは住宅価格を予測する回帰問題で、説明変数としては数値変数とカテゴリ変数が混在しています。予測対象の目的変数は住宅の販売価格(SalePrice)、特徴量は80変数、データ件数は1460件です。
データの最初の5件は以下の通り。
| Id | MSSubClass | MSZoning | LotFrontage | LotArea | Street | Alley | LotShape | LandContour | Utilities | LotConfig | LandSlope | Neighborhood | Condition1 | Condition2 | BldgType | HouseStyle | OverallQual | OverallCond | YearBuilt | YearRemodAdd | RoofStyle | RoofMatl | Exterior1st | Exterior2nd | MasVnrType | MasVnrArea | ExterQual | ExterCond | Foundation | BsmtQual | BsmtCond | BsmtExposure | BsmtFinType1 | BsmtFinSF1 | BsmtFinType2 | BsmtFinSF2 | BsmtUnfSF | TotalBsmtSF | Heating | HeatingQC | CentralAir | Electrical | 1stFlrSF | 2ndFlrSF | LowQualFinSF | GrLivArea | BsmtFullBath | BsmtHalfBath | FullBath | HalfBath | BedroomAbvGr | KitchenAbvGr | KitchenQual | TotRmsAbvGrd | Functional | Fireplaces | FireplaceQu | GarageType | GarageYrBlt | GarageFinish | GarageCars | GarageArea | GarageQual | GarageCond | PavedDrive | WoodDeckSF | OpenPorchSF | EnclosedPorch | 3SsnPorch | ScreenPorch | PoolArea | PoolQC | Fence | MiscFeature | MiscVal | MoSold | YrSold | SaleType | SaleCondition | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 60 | RL | 65 | 8450 | Pave | nan | Reg | Lvl | AllPub | Inside | Gtl | CollgCr | Norm | Norm | 1Fam | 2Story | 7 | 5 | 2003 | 2003 | Gable | CompShg | VinylSd | VinylSd | BrkFace | 196 | Gd | TA | PConc | Gd | TA | No | GLQ | 706 | Unf | 0 | 150 | 856 | GasA | Ex | Y | SBrkr | 856 | 854 | 0 | 1710 | 1 | 0 | 2 | 1 | 3 | 1 | Gd | 8 | Typ | 0 | nan | Attchd | 2003 | RFn | 2 | 548 | TA | TA | Y | 0 | 61 | 0 | 0 | 0 | 0 | nan | nan | nan | 0 | 2 | 2008 | WD | Normal |
| 1 | 2 | 20 | RL | 80 | 9600 | Pave | nan | Reg | Lvl | AllPub | FR2 | Gtl | Veenker | Feedr | Norm | 1Fam | 1Story | 6 | 8 | 1976 | 1976 | Gable | CompShg | MetalSd | MetalSd | None | 0 | TA | TA | CBlock | Gd | TA | Gd | ALQ | 978 | Unf | 0 | 284 | 1262 | GasA | Ex | Y | SBrkr | 1262 | 0 | 0 | 1262 | 0 | 1 | 2 | 0 | 3 | 1 | TA | 6 | Typ | 1 | TA | Attchd | 1976 | RFn | 2 | 460 | TA | TA | Y | 298 | 0 | 0 | 0 | 0 | 0 | nan | nan | nan | 0 | 5 | 2007 | WD | Normal |
| 2 | 3 | 60 | RL | 68 | 11250 | Pave | nan | IR1 | Lvl | AllPub | Inside | Gtl | CollgCr | Norm | Norm | 1Fam | 2Story | 7 | 5 | 2001 | 2002 | Gable | CompShg | VinylSd | VinylSd | BrkFace | 162 | Gd | TA | PConc | Gd | TA | Mn | GLQ | 486 | Unf | 0 | 434 | 920 | GasA | Ex | Y | SBrkr | 920 | 866 | 0 | 1786 | 1 | 0 | 2 | 1 | 3 | 1 | Gd | 6 | Typ | 1 | TA | Attchd | 2001 | RFn | 2 | 608 | TA | TA | Y | 0 | 42 | 0 | 0 | 0 | 0 | nan | nan | nan | 0 | 9 | 2008 | WD | Normal |
| 3 | 4 | 70 | RL | 60 | 9550 | Pave | nan | IR1 | Lvl | AllPub | Corner | Gtl | Crawfor | Norm | Norm | 1Fam | 2Story | 7 | 5 | 1915 | 1970 | Gable | CompShg | Wd Sdng | Wd Shng | None | 0 | TA | TA | BrkTil | TA | Gd | No | ALQ | 216 | Unf | 0 | 540 | 756 | GasA | Gd | Y | SBrkr | 961 | 756 | 0 | 1717 | 1 | 0 | 1 | 0 | 3 | 1 | Gd | 7 | Typ | 1 | Gd | Detchd | 1998 | Unf | 3 | 642 | TA | TA | Y | 0 | 35 | 272 | 0 | 0 | 0 | nan | nan | nan | 0 | 2 | 2006 | WD | Abnorml |
| 4 | 5 | 60 | RL | 84 | 14260 | Pave | nan | IR1 | Lvl | AllPub | FR2 | Gtl | NoRidge | Norm | Norm | 1Fam | 2Story | 8 | 5 | 2000 | 2000 | Gable | CompShg | VinylSd | VinylSd | BrkFace | 350 | Gd | TA | PConc | Gd | TA | Av | GLQ | 655 | Unf | 0 | 490 | 1145 | GasA | Ex | Y | SBrkr | 1145 | 1053 | 0 | 2198 | 1 | 0 | 2 | 1 | 4 | 1 | Gd | 9 | Typ | 1 | TA | Attchd | 2000 | RFn | 3 | 836 | TA | TA | Y | 192 | 84 | 0 | 0 | 0 | 0 | nan | nan | nan | 0 | 12 | 2008 | WD | Normal |
前処理
実験用としてとりあえず最初に、欠損値の処理として、数値変数には中央値を、カテゴリ変数には “missing” という文字列を補完しました。
実験用に特徴量を機械的に増やす
今回の80個の特徴量から、無理やり特徴量を増やす前処理を次のように行いました。
特徴量を増やす処理
- カテゴリ変数はすべてone-hotエンコーディングを実施
- 数値変数どうしの組み合わせ(自己積を含む)で積により生成
- one-hot後のカテゴリ変数(ダミー変数)と数値変数の全ての組み合わせについて積により生成
- 数値変数は標準化処理を実施
- 以上の処理により特徴量数は9,290となった。
以上の処理で9,290個の特徴量に増加させることができました!
実験結果
結果は以下でした。
| モデル | 特徴量数 | 学習データ R2 | 検証データ R2 | 変数選択 の秒数 |
|---|---|---|---|---|
| 特徴量削減なしベースラインモデル | 9290 | 1.00 | 0.83 | 2.1 |
| F値選択法:50個選択 | 50 | 0.87 | 0.87 | 0.4 |
| F値選択法:100個選択 | 100 | 0.89 | 0.86 | 0.4 |
| F値選択法:150個選択 | 150 | 0.91 | 発散※1 | 0.4 |
| Lasso回帰ベース選択法:50個選択 | 50 | 0.76 | 0.41 | 7.3 |
| Lasso回帰ベース選択法:100個選択 | 100 | 0.89 | 0.77 | 7.0 |
| Lasso回帰ベース選択法:150個選択 | 150 | 0.92 | 0.79 | 7.0 |
| 決定木ベース選択法:50個選択 | 50 | 0.88 | 0.87 | 0.5 |
| 決定木ベース選択法:100個選択 | 100 | 0.91 | 0.88 | 0.5 |
| 決定木ベース選択法:150個選択 | 150 | 0.93 | 0.65 | 0.7 |
| ランダムフォレストベース選択法:50個選択 | 50 | 0.90 | 0.89 | 75.3 |
| ランダムフォレストベース選択法:100個選択 | 100 | 0.92 | 0.90 | 69.5 |
| ランダムフォレストベース選択法:150個選択 | 150 | 0.93 | 0.91 | 69.4 |
| 再帰的特徴量選択法(重回帰ベース)※2 | – | – | – | – |
| 前向き逐次特徴量選択法(重回帰ベース)※2 | – | – | – | – |
※注1:推定がうまくいかず、計算不可
※注2:10分以上実行しても終了せず、処理を中断
それぞれ、みていきましょう。
決定係数R2値の比較
以下は学習データと検証データにおける決定係数R2値の比較です。決定係数は重回帰モデルなどで利用できるモデルの評価指標で、-♾️〜1の値を取り、1の場合データに対してモデルが完璧にフィットしているモデルになります。
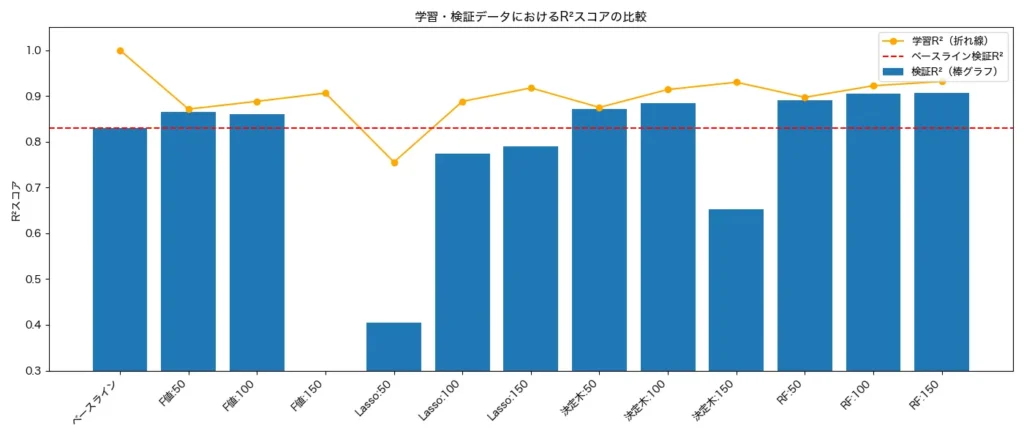
まずベースラインの全変数を投入した回帰モデルについては学習データではR2値は1となり完璧にモデルがデータにフィットしています。一方で、検証データではR2値は0.83と落ち込んでおり、典型的な過学習といえます。
また、赤線はベースモデルの検証データのR2値であり、この値よりも上回っていたら特徴量選択の効果が出ていると言えるでしょう。こうやってみると、F値による選択法(50個、100個)、決定木による選択法(50個、100個)、ランダムフォレストによる選択法(50個、100個、150個)でベースモデルを上回っています。特にランダムフォレストは(50個、100個、150個)の全てでベースモデルを上回っており過学習を回避しており、またR2値も他の選択方より高く、非常に優秀な選択法であることが見て取れます。
ちなみに、再帰的特徴量選択法と逐次選択法はどちらも10分以上たっても結果が帰ってこず、処理を断念しました。今回試しにやってみたところ、どちらも30変数くらいだとサクサク結果を出し、またその性能は非常に高かったのですが、それ以上になると急に処理が帰ってこなくなりました。そのためこの2つの選択法は30変数程度の小規模の特徴量選択では抜群に性能はよいものの、100以上の特徴量を有するようなビッグデータに対する選択法としては実用上は難しいでしょう。
処理スピードによる比較
以下は変数選択に要した処理スピード(秒)の比較です。
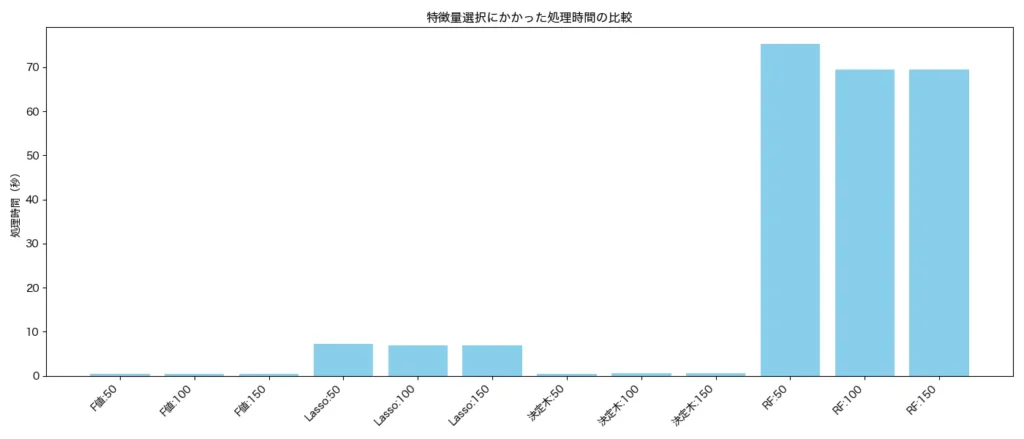
F値や決定木ベースの選択法ではほぼ所要時間はかかっていません。ランダムフォレストについては1分程度かかっています。
結論とおすすめの使用例
今回や約1万個の特徴量から50~150程度に特徴量を選択し、過学習の防止と予測精度の向上のための実験を行なってみました。以上から僕なりの結論が以下となります。
精度を上げるための、おすすめの特徴量選択法
ランダムフォレストベース特徴量選択は非常におすすめ!他の選択法に比べ過学習になりにくく、検証データでの予測精度も高く、めちゃめちゃ安定している。ただし、実行時間はかかる。
スピーディーに実施したい場合のおすすめ特徴量選択法
決定木ベースの特徴量選択方はかなりスピーディーに実行できる割に、過学習もしにくくとてもよい!時点でF値による選択法もなかなかよい。
僕なりの特徴量選択のおすすめ手順
もし、データに対して事前知識や仮説がなくとりあえず、特徴量を生成しなければならない場合は、まず、考えられる特徴量を機械的に作ってしまっていいでしょう。その後、大まかに予測で使うモデル(重回帰モデルとかLightGBMとか、ランダムフォレストとか)を決定しましょう。(ここでいう「予測で使うモデル」というのは、特徴量選択で使用するモデルベースの予測モデルではなく、特徴量選択した後の実際の予測を実行するためのモデルのことです)
そして、その予測で使うモデルがどの程度の特徴量の数だったらどの程度の時間がかかるのかとか、予測が発散するのか実験し、許容できる特徴量の数について、事前にあたりをつけてみましょう。
たとえば、今回の実験におけるデータで今回の予測モデルである重回帰モデルだと50〜150個の特徴量の数を、大まかな目安として掲げました。こんな感じで「100個で実行、200個で実行、300個で実行」という感じでざっくりと事前に実験してみて「300個くらいが処理時間で許容できる限界かな」とか「500個くらいが予測精度の向上の頭打ちかな」とか「800個以上だと推定値が発散するな」みないなざっくりとした目安を、事前に確認することをがとても重要です。
その後、目安となる特徴量の個数を選択するよう特徴量選択のプログラムを実行します。
ちなみに、特徴量の数は自動的に取捨選択できないこともないですが、僕は人間の手で特徴量の数を指定することをお勧めします。というのも、モデルベースでの特徴量選択を実施する場合、最適な特徴量の個数まで推定する機能は、逐次選択法や再帰的選択法に比べ劣っています。そのため、僕の経験上、ビッグデータを対象とした場合、特徴量の個数については人間がおおよそのあたりをつけた方がよいケースが多いからです。
この手順でモデルの構築を進めていき、最終的なモデルを構築する時点で特徴量の個数を微調整していけばいいでしょう。
筆者のおすすめする特徴量選択手順
- 考えられる特徴量選択はとりあえず機械的に作る
- 予測モデルを決める
- その予測モデルで使う特徴量の数をざっくりと実験(精度の観点や処理時間の観点から)
- 使用する特徴量の数をざっくりと決定する
- モデルベースの特徴量選択法で、上で決めた特徴量の数を選択してみる(特徴量の数は人間が指定する)
- モデル構築を実施
- その後最終モデルで特徴量の数などは微調整する
ちなみに、pythonのscikit-learnの特徴量選択ライブラリで、モデルベースでの特徴量選択を実行する際、特徴量の数を指定する場合はちょっとしたコツが必要なので、気になる方は、後のpythonプログラムを参照してください。
参考:pythonプログラム
今回は次のように重回帰モデルで予測を実施し実験しました。
import numpy as np
import pandas as pd
import time
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score, mean_squared_error
def run_feature_selection_experiment(X, y, title,selector=None, test_size=0.3, random_state=42):
"""
特徴量選択 → 重回帰モデル学習 → 学習/検証スコア計算 + 実行時間表示
"""
start_time = time.time() # 開始時刻の記録
# 学習・検証データに分割
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=test_size, random_state=random_state
)
if selector is not None:
# 特徴量選択(学習データに対して fit → transform)
X_train_sel = selector.fit_transform(X_train, y_train)
X_test_sel = selector.transform(X_test)
len_features = len(selector.get_support(indices=True))
else:
X_train_sel = X_train
X_test_sel = X_test
len_features = X_train.shape[1]
# モデル学習(重回帰)
model = LinearRegression()
model.fit(X_train_sel, y_train)
# 予測
y_pred_train = model.predict(X_train_sel)
y_pred_test = model.predict(X_test_sel)
# スコア計算
train_score = r2_score(y_train, y_pred_train)
test_score = r2_score(y_test, y_pred_test)
end_time = time.time() # 終了時刻の記録
elapsed_time = end_time - start_time
# 出力
print(f"Train R²: {train_score:.3f}")
print(f"Test R²: {test_score:.3f}")
print(f"選択された特徴量数: {len_features}")
print(f"処理時間: {elapsed_time:.2f} 秒")
return {
"title": title,
"X_train_shape": X_train_sel.shape,
"X_test_shape": X_test_sel.shape,
"train_r2": train_score,
"test_r2": test_score,
"train_mse": train_mse,
"test_mse": test_mse,
"train_rmse": train_rmse,
"test_rmse": test_rmse,
"selected_features": len_features,
"time_sec": elapsed_time
}
特徴量選択の実行とモデルによる予測の実行は以下のプログラムです。公式マニュアルの特徴量選択についてはこちらから参照してください。
from sklearn.feature_selection import VarianceThreshold, SelectKBest, GenericUnivariateSelect, SelectFromModel
from sklearn.feature_selection import RFECV, SequentialFeatureSelector
from sklearn.linear_model import LinearRegression, Lasso
from sklearn.feature_selection import f_regression
from sklearn.model_selection import KFold
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
title = "すべての特徴量を投入"
list_output = []
# 特徴量選択なし
print("")
print("------------------------")
print("特徴量選択なし")
res = run_feature_selection_experiment(X, y, title + "特徴量選択なし")
list_output.append(res)
# F値による単変量選択(F値の高い特徴量をk個選ぶ)
selector = SelectKBest(score_func=f_regression, k=50)
print("")
print("------------------------")
print("F値による特徴量選択")
res = run_feature_selection_experiment(X, y, title +"F値による特徴量選択:50" ,selector)
list_output.append(res)
# F値による単変量選択(F値の高い特徴量をk個選ぶ)
selector = SelectKBest(score_func=f_regression, k=100)
print("")
print("------------------------")
print("F値による特徴量選択")
res = run_feature_selection_experiment(X, y, title +"F値による特徴量選択:100" ,selector)
list_output.append(res)
# F値による単変量選択(F値の高い特徴量をk個選ぶ)
selector = SelectKBest(score_func=f_regression, k=150)
print("")
print("------------------------")
print("F値による特徴量選択")
res = run_feature_selection_experiment(X, y, title +"F値による特徴量選択:150" ,selector)
list_output.append(res)
# モデルベース(Lasso)による特徴量選択
selector_model = SelectFromModel(estimator=Lasso(alpha=0.01, max_iter=10000),max_features=50)
print("")
print("------------------------")
print("モデルベース(Lasso)による特徴量選択")
res = run_feature_selection_experiment(X, y, title +"モデルベース(Lasso):50", selector_model)
list_output.append(res)
# モデルベース(Lasso)による特徴量選択
selector_model = SelectFromModel(estimator=Lasso(alpha=0.01, max_iter=10000),max_features=100)
print("")
print("------------------------")
print("モデルベース(Lasso)による特徴量選択")
res = run_feature_selection_experiment(X, y, title +"モデルベース(Lasso):100", selector_model)
list_output.append(res)
# モデルベース(Lasso)による特徴量選択
selector_model = SelectFromModel(estimator=Lasso(alpha=0.01, max_iter=10000),max_features=150)
print("")
print("------------------------")
print("モデルベース(Lasso)による特徴量選択")
res = run_feature_selection_experiment(X, y, title +"モデルベース(Lasso):150", selector_model)
list_output.append(res)
selector_model = SelectFromModel(
estimator=DecisionTreeRegressor(max_depth=4,random_state=42),
max_features=50,
threshold=-np.inf
)
print("")
print("------------------------")
print("モデルベース(決定木)による特徴量選択")
res = run_feature_selection_experiment(X, y, title +"モデルベース(Tree):50",selector_model)
list_output.append(res)
selector_model = SelectFromModel(
estimator=DecisionTreeRegressor(max_depth=4,random_state=42),
max_features=100,
threshold=-np.inf
)
print("")
print("------------------------")
print("モデルベース(決定木)による特徴量選択")
res = run_feature_selection_experiment(X, y, title +"モデルベース(Tree):100",selector_model)
list_output.append(res)
selector_model = SelectFromModel(
estimator=DecisionTreeRegressor(max_depth=4,random_state=42),
max_features=150,
threshold=-np.inf
)
print("")
print("------------------------")
print("モデルベース(決定木)による特徴量選択")
res = run_feature_selection_experiment(X, y, title +"モデルベース(Tree):150",selector_model)
list_output.append(res)
# モデルベース(ランダムフォレスト)による特徴量選択
selector_model = SelectFromModel(
estimator=RandomForestRegressor(n_estimators=150, random_state=42),
max_features=50,
threshold=-np.inf
)
res = run_feature_selection_experiment(X, y, title +"ランダムフォレスト:50",selector_model)
list_output.append(res)
# モデルベース(ランダムフォレスト)による特徴量選択
selector_model = SelectFromModel(
estimator=RandomForestRegressor(n_estimators=150, random_state=42),
max_features=100,
threshold=-np.inf
)
res = run_feature_selection_experiment(X, y, title +"ランダムフォレスト:100",selector_model)
list_output.append(res)
# モデルベース(ランダムフォレスト)による特徴量選択
selector_model = SelectFromModel(
estimator=RandomForestRegressor(n_estimators=150, random_state=42),
max_features=150,
threshold=-np.inf
)
res = run_feature_selection_experiment(X, y, title +"ランダムフォレスト:150",selector_model)
list_output.append(res)
# 再帰的特徴量削減(RFECV)
selector_rfecv = RFECV(
estimator=LinearRegression(),
step=1,
cv=KFold(n_splits=5),
scoring='r2',
min_features_to_select=10 # 適宜調整可能
)
run_feature_selection_experiment(X, y, selector_rfecv)
# 逐次特徴量選択(前向き)
selector_sfs = SequentialFeatureSelector(
estimator=LinearRegression(),
direction='forward',
cv=KFold(n_splits=5),
n_features_to_select="auto" # 'auto' で自動選択(sklearn 1.3+)
)
run_feature_selection_experiment(X_step1, y, selector_sfs)
list_output
with open(f"output/feature_selection_{title}.txt", "w") as f:
for res in list_output:
f.write(str(res) + "\n")
特徴量の数を指定するコツ
F値による特徴量の数を指定する場合、以下のようにsklearのSelectKBestを使うと簡単に指定できます。以下はscore_func=f_regressionで、回帰予測であること(連続変数を予測するケースであること)を指定し、k=150で150個の特徴量を指定する例です。
selector = SelectKBest(score_func=f_regression, k=150) モデルベースの特徴量選択で、選ぶ特徴量の数を指定したい場合は以下となります。
selector_model = SelectFromModel(
estimator=DecisionTreeRegressor(max_depth=4,random_state=42),
max_features=100,
threshold=-np.inf
)
特徴量の数の最大値は max_features を使って指定できます。たとえば、estimator に決定木を指定し、max_features=100 とすると、「重要度の高い順に最大100個の特徴量を選ぶ」という設定になります。
ただし、ここで注意が必要なのが threshold の設定です。何も指定しない場合は、デフォルトで「重要度が平均以上」の特徴量しか選ばれません。つまり、max_features=100 としても、平均未満の重要度の特徴量が自動的に除外されるため、結果として100個より少なくなってしまうことがあります。
これを避けるためには、threshold=-np.inf と設定することで、「重要度による足切りを一切しない」ようにします。これにより、全ての特徴量が選考対象となり、max_features の設定どおりに希望の数だけ選ばれるようになります。モデルベースの特徴量選択を使う際は、この threshold の指定がとても重要です。
まとめ
今回は、特徴量選択について、長々となりましたが解説しました。実験も実施し、特徴量選択のためのちょっとした指針も示せたのではと思います。ぜひ、参考にして下さい!
