pythonによる回帰分析〜重回帰モデル入門

2025年3月9日2025年4月10日

こんにちは、デジタルボーイです。前回は機械学習や統計モデルの初めの一歩とも言える、単回帰分析について学習しました。

あわせて読みたい

pythonによる回帰分析、初歩の初歩〜単回帰モデルこんにちは、デジタルボーイです。今回は機械学習や統計モデルの初めの一歩とも言える、単回帰分析について、Pythonとscikit-learnを使い、初歩の初歩について解説した…

データ分析を始めたばかりの方にとって、複数の要因が影響する問題を予測するのは少し難しく感じるかもしれません。しかし、「重回帰モデル」を使えば、複数の特徴量を考慮してより正確な予測が可能になります。本記事では、重回帰モデルのメカニズムの直感的な理解をするよう解説し、最後に、Scikit-learn（sklearn）を使って重回帰モデルを実装し、視覚的にその動作を理解できるように解説します！

記事を書いた人

デジタルボーイです。
データサイエンス歴20年以上のおっさんです。中小企業診断士として、データサイエンス、WEBマーケティング、SEOに関するデータ分析、コンサルティングの仕事をしています。自己紹介の詳細はコチラ

重回帰モデルとは？

重回帰分析は、複数の要因（変数）がある中で、それらがどのように結果に影響を与えているかを明らかにするための統計手法です。たとえば、「家の価格」に影響する要因として「広さ」「築年数」「駅からの距離」などが考えられますが、重回帰分析を使えば、これら複数の要素が価格にどう関係しているのかを数式で表現できます。

ちなみに、最も基本的なのが「単回帰分析」で、これは「一つの原因が結果にどのように影響するか」を調べます。一方で「重回帰分析」は「複数の原因がある」ケースを扱います。

重回帰分析の目的

重回帰分析の主な目的は、「結果に最も影響を与えている要因はどれか」を明らかにすることです。ただし単に相関を見るだけではなく、「他の条件が同じならこの要因はどの程度の影響を与えているか」という“独立した効果”を評価できるのが大きな特徴です。

たとえば、中古物件の価格に影響する要因として「敷地面積」「建物面積」「築年数」「駅からの距離」「学区の評価」「騒音レベル」などがあるとします。重回帰分析を使えば、「駅からの距離や学区の評価が同じであると仮定したとき、築年数が価格にどれだけ影響するのか」といった、各要因の独立した影響を明らかにすることができます。

モデル式の読み解き方

重回帰分析では、上の中古物件の価格予測モデルを次のように数式で表します。

Y = β0 + β1 × [敷地面積] + β2 ×[建物面積] + β3 × [築年数] +
β4 × [駅からの距離] + β5 × [学区の評価] + β6 × [騒音レベル] + ε

β0は切片と言い、β1〜β6は回帰係数と言い、εは誤差と言います。βxが回帰モデルのパラメータと言い、このパラメータで手元のデータから予測をしようと言うのが、重回帰分析の考え方になります。仮にソフトウェアで分析を実行した場合、例えば、次のようにβが予測されます。

価格 = 500 + 0.8 × [敷地面積] + 1.2 × [建物面積] – 0.6 × [築年数]
– 1.5 × [駅からの距離] + 2.0 × [学区の評価] – 1.0 × [騒音レベル] + ε

ここで、各変数の単位は以下のように仮定します。

敷地面積・建物面積：平方メートル（㎡）
築年数：年
駅からの距離：分
学区の評価：1〜5のスコア
騒音レベル：1〜10のスコア

このモデルを解釈すると、例えば「建物面積が1㎡増えると、他の条件が同じであれば物件価格は約1.2万円上がる」ことを意味します。同様に、「築年数が1年古くなると、他の条件が同じであれば価格は0.6万円下がる」、「学区の評価が1ランク上がると他の条件が同じであれば価格は2万円上がる」など、各変数の影響を個別に読み解くことができます。

このように、重回帰分析の回帰係数（偏回帰係数）は「他の変数を一定に保ったとき、その変数が目的変数にどれだけ影響するか」を表しており、各要因の“独立した効果”を理解するための鍵となります。

パラメータ（係数）はどうやって決まるのか？

重回帰分析では、各変数にかかる係数（β）を「過去のデータに最もよく合うように」自動的に計算して決めます。

これは「最小二乗法」という方法で行われます。イメージしやすいように、まずは単回帰モデルの散布図を考えてみましょう。データ点が散らばっていて、その中を一本の直線（回帰直線）が通っています。そして、各データ点からこの直線に向けて引いた垂線の長さが「誤差」です。

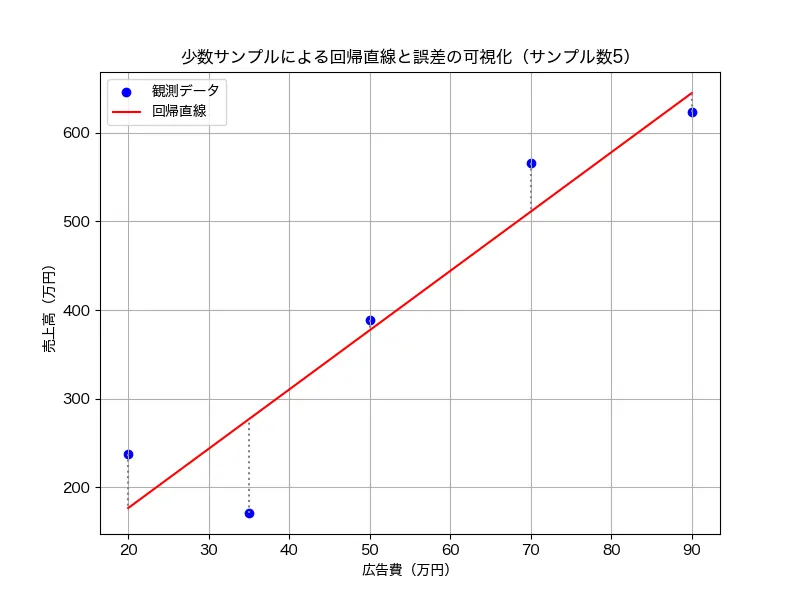
この誤差がすべての点でできるだけ短くなるように、つまり、すべての垂線の長さの二乗を合計した値が最も小さくなるように、コンピュータが係数（β）の値を調整していくのです。

ちなみに、場違いな回帰直線を引いた場合、点と垂線は次のように長くなります。

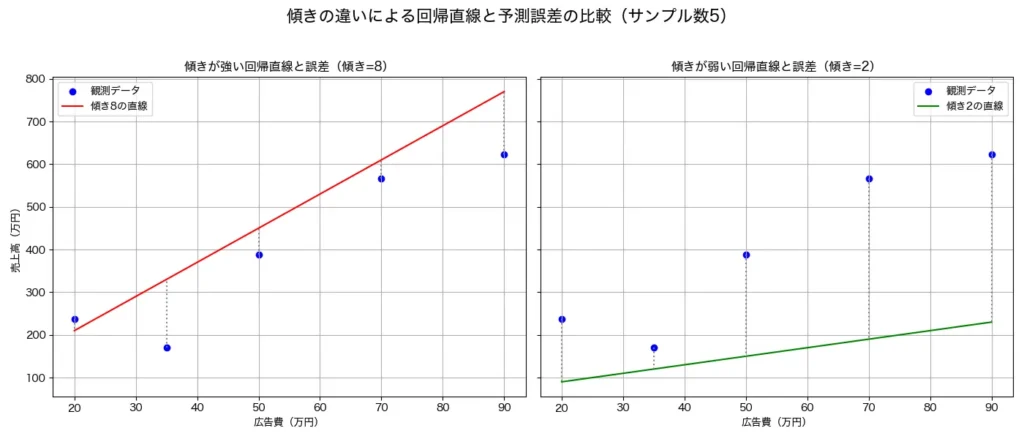
重回帰分析でも基本的な考え方は同じで、多次元の空間における予測と実測値の誤差（＝垂線の距離）を最小にするようにモデルが構築されます。つまり、重回帰分析は「どうすれば誤差が最小になるか？」という視点で、各要因の影響力（偏回帰係数）を導き出しているということです。

重回帰分析の注意点

便利な分析手法ではありますが、注意すべき点もあります。

多重共線性

説明変数同士の関係性が強すぎると（これを多重共線性と呼びます）、それぞれの変数が独立して価格にどう影響しているかをうまく判断できなくなります。

たとえば「築年数」と「居住年数」がほとんど同じような値を持つとき、これらはモデルの中でほぼ同じ情報を持つことになります。

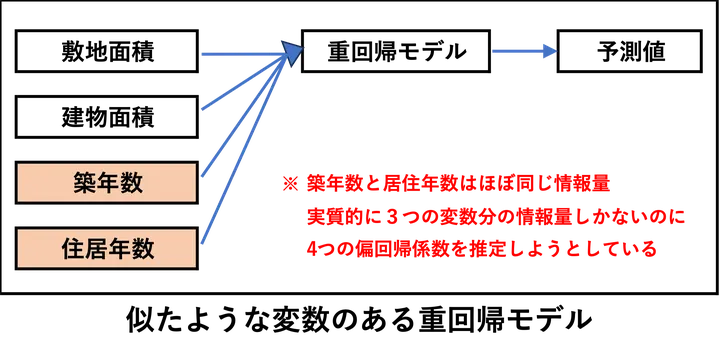
上図の場合、重回帰モデルに入力されるデータは4つの変数のようにも見えますが、「築年数」と「居住年数」は実質的に同じ変数のため、3つの変数とみなされます。にもかかわらず、4つの変数分の回帰係数を推定しようとした場合、「３本分の情報しかないのに４本分のパラメータを推定しようとする」こととなります。このように、n個の変数に見えても、実際にはn-1個分の独立した情報しかなければ、情報が不足していて、数学的に答えが一意に決まりにくくなるのです。

その結果、係数（β）の値が極端に大きくなったり、ほんの少しデータが変わるだけで推定値が大きく変わったりして、モデル全体が不安定になります。これが「パラメータが推定しにくくなる」という状態におちいります。同じようなデータは事前に排除することが必要です。

相関関係と因果関係

また、重回帰分析が示すのはあくまで「関係性（相関）」であり、「因果関係」そのものを証明するものではありません。

別の例として、「アイスクリームの売上」と「熱中症の救急搬送件数」が正の関係にあるとします。統計的にはどちらも気温が上がると増えるため、相関は成立します。

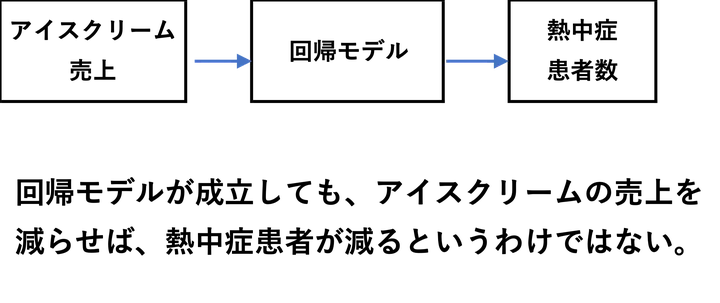
しかし、もし、熱中症患者の増加を気に掛けたA市の市長が「これ以上熱中症患者を増やさないために、アイスクリームの販売は禁止しよう！」という政策を掲げようとした場合、あなたがこの市長の秘書であれば、頭を引っ叩いてもこの政策に反対すべきですし、それでもダメなら、できるだけ早く辞表を提出した方が賢明です。

というのも、当たり前ですが、この関係を見て「アイスクリームの販売を減らせば、熱中症患者は減る」と考えるのは誤りです。仮に人為的にアイスクリームの売上だけを調整しても、熱中症の件数には影響しないはずです。

このように、回帰式が成り立っても「Aを増やせばBが変わる」という因果関係があるとは限らない、という点に注意が必要です。

外れ値に敏感

さらに、単回帰分析や重回帰分析は外れ値（ごく一部の極端なデータ）に対して敏感です。たった1つの異常な価格の物件が、モデル全体に大きな影響を与えてしまうこともあります。以下は10個のダミーデータで、右のグラフだけ、最後の1件のデータをY軸方向に極端に大きくした例です。

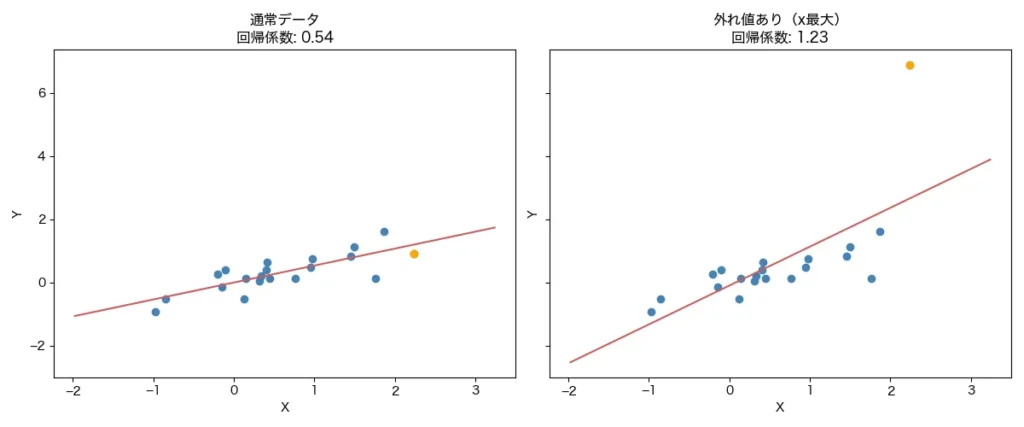
9件のデータは同じでも1件のデータが極端に外れた場合、回帰直線はかなり違っています。このように極端な値に回帰直線は引っ張られやすい性質があります。外れ値についてはぜひ、事前に散布図などで確認しましょう。

外れ値の除去については以下に詳しく解説してあるので、参考にしてください。

あわせて読みたい

予測精度を上げる！欠損値と外れ値の処理テクニックまとめこんにちは、デジタルボーイです。今回は予測精度をあげるための欠損値と外れ値の処理テクニックについて、Pythonプログラミングを使いながら解説したいと思います。記…

必要なライブラリとインストール方法

それでは、実際にPythonで回帰分析を実行してみましょう。まずは必要なライブラリを読み込みましょう。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.datasets import fetch_california_housing

もし、必要なライブラリがインストールされていない場合は、pipでインストールしておきましょう。

pip install numpy pandas matplotlib scikit-learn

pipを使ったインストール方法はこちらになります。

あわせて読みたい

pipでpandasをインストールする方法こんにちは、デジタルボーイです。備忘録がてら、macとLinuxにpipでpandasをインストールするための手順を、まとめておきます。記事を書いた人デジタルボーイです。デ…

あわせて読みたい

pipでnumpyをインストールする方法こんにちは、デジタルボーイです。備忘録がてら、macとLinuxにpipでNumPyをインストールするための手順を、まとめておきます。記事を書いた人デジタルボーイです。デ…

あわせて読みたい

pipでscikit-learn(sklearn)をインストールする方法：こんにちは、デジタルボーイです。備忘録がてら、macとLinuxにpipでscikit-learn(sklearn)をインストールするための手順を、まとめておきます。記事を書いた人デジタ…

データの読み込みと概要の確認

Scikit-learnの「California housing dataset（カリフォルニア住宅価格データ）」を使用します

# データを取得
data = fetch_california_housing()
df = pd.DataFrame(data.data, columns=data.feature_names)
df["Price"] = data.target  # 住宅価格を追加

# データの概要を表示
print(df.head())
print(df.describe())

コードの解説

fetch_california_housing() でScikit-learnの住宅データを取得
pd.DataFrame() でデータをPandasのデータフレームに変換
df["Price"] = data.target で住宅価格を追加
head() でデータの先頭5行を表示
describe() で統計情報（平均値・標準偏差・最大値など）を確認

データの初めの５件はこんな感じです。

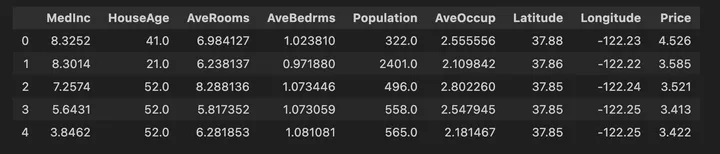
データの統計情報は以下のように出力されました。

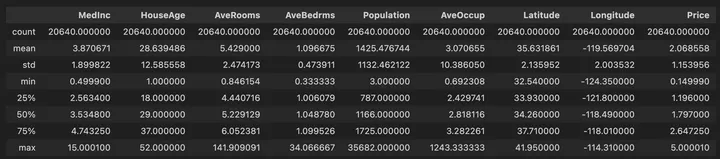
分析の目的とゴール

では、実際のこのデータを使って分析してみましょう。

目的：
住宅価格に影響を与える要因（年収、部屋数、築年数など）を分析し、価格を予測するモデルを作成する。

ゴール：

特徴量の影響を直感的に理解する
重回帰モデルを作成し、予測精度を評価する
結果をグラフ化し、モデルの出力を解釈する

データの可視化

まず、いくつかの特徴量と価格の関係を可視化してみます。

plt.rcParams["font.family"] = "Hiragino sans"

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.scatter(df["MedInc"], df["Price"], alpha=0.5)
plt.xlabel("年収中央値 (MedInc)")
plt.ylabel("住宅価格 (Price)")
plt.title("年収と住宅価格の関係")

plt.subplot(1, 2, 2)
plt.scatter(df["AveRooms"], df["Price"], alpha=0.5, color='red')
plt.xlabel("平均部屋数 (AveRooms)")
plt.ylabel("住宅価格 (Price)")
plt.title("平均部屋数と住宅価格の関係")

plt.show()

コードの解説

plt.rcParams["font.family"] = "Hiragino sans"でMac用の日本語フォントをを指定。Windowsの場合は、plt.rcParams[“font.family”] = “Meiryo”などにする。
plt.figure(figsize=(12, 5)) でグラフのサイズを指定
plt.subplot(1, 2, 1)は、１枚のプロット画像に複数のグラフ（サブプロット）を描画するための指定。具体的には、カッコ内の数値で「１行2列の1番目にプロットしなさい」という指定。以降に出てくるplt.subplot(1, 2, 2)は「１行2列の２番目にプロットしなさい」という指定。
plt.scatter() で散布図を描画
alpha=0.5 で透明度を設定し、データの密集度を見やすくする
subplot() を使って複数のグラフを並べて表示

アウトプットはこんな感じです。

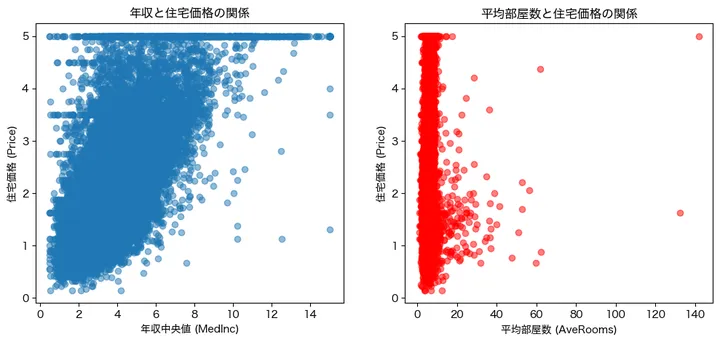
左側のグラフは年収と住宅価格の関係性をプロットしたものです。縦軸の住宅価格は1,2,3,4,5となっています、おそらく10万ドル単位なのでしょう。また、５のところ（50万ドル）のところで上限が切られているようですね。本来は５以上のデータとして持っているのでしょうが、上限を５に置き換えたデータとしているようです。概ね、収入が上がれば上がるほど、住宅価格は高くなる傾向が見えました。

右側は部屋数と住宅価格のプロットです。０から１０くらいの部屋数にびっしりとデータが詰まっているようで、一見するとそれほど関係性は高くなさそうですね。

重回帰モデルの作成と学習

それでは、すべての特徴量を使って、重回帰モデルを作成してみましょう。

# 特徴量とターゲットを設定
X = df.drop(columns=["Price"])  # すべての特徴量を使用
y = df["Price"]

# 訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# モデルの作成と学習
model = LinearRegression()
model.fit(X_train, y_train)

# 予測
y_pred = model.predict(X_test)

コードの解説

drop(columns=["Price"]) で目的変数（住宅価格）を除外し、特徴量だけをXに設定
train_test_split() でデータを訓練用とテスト用に分割（80%:20%）
LinearRegression() で重回帰モデルを作成
fit() でモデルを学習
predict() でテストデータを予測

モデルの評価

続いて、構築したモデルの精度をMSE、RMSE、決定係数（R²）で評価してみましょう。

# 評価指標の計算
mse = mean_squared_error(y_test, y_pred)
rmse = np.sqrt(mse)
r2 = r2_score(y_test, y_pred)

print(f"Mean Squared Error (MSE): {mse:.2f}")
print(f"Root Mean Squared Error (RMSE): {rmse:.2f}")
print(f"R² Score: {r2:.2f}")

コードの解説

mean_squared_error() でMSE（誤差の2乗の平均）を計算
np.sqrt(mse) でRMSE（MSEの平方根）を計算し、誤差の大きさを直感的に理解しやすくする
r2_score() で決定係数（R²）を計算し、モデルの説明力を評価（1に近いほど良いモデル）

結果はこんな感じでした。

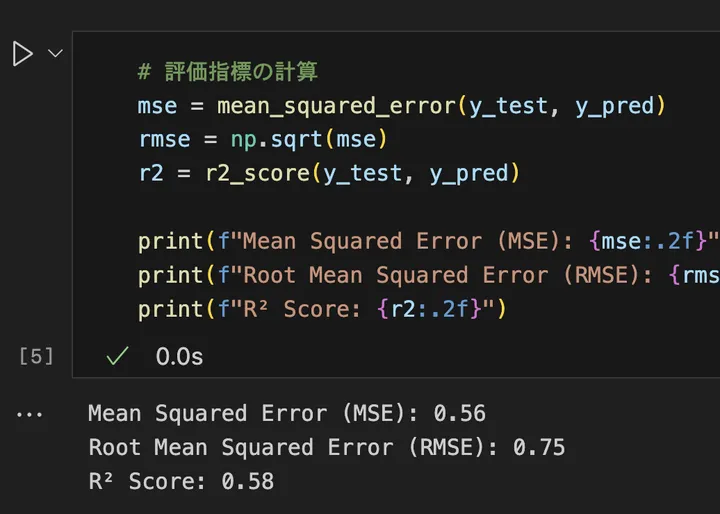
簡単に、それぞれの評価指標についてみていきましょう。

MSE（平均二乗誤差）は、予測値と実際の値の差を二乗し、それらの平均を取ったものです。数値が小さいほどモデルの誤差が少なく、より正確に予測できていることを意味します。ただし、単位が元のデータの単位の二乗になってしまうため、直感的に解釈しにくいという欠点があります。

RMSE（ルート平均二乗誤差）は、MSEの平方根を取ったものです。MSEと異なり、元のデータと同じ単位になるため、直感的に理解しやすくなります。例えば、住宅価格を予測する場合、RMSEが10万円であれば、平均的に10万円の誤差があると解釈できます。値が小さいほど予測の精度が高いことを意味します。

決定係数（R²）は、モデルがどれだけデータをうまく説明できているかを示す指標です。値は0から1の範囲を取り、1に近いほどモデルの予測が正確であることを示します。0に近い場合は、「単に平均値を予測するのと変わらない」ことを意味し、モデルの説明力が低いことを示します。一般的に0.7以上であれば良いモデルと考えられます。今回のモデルの結果から、R²スコア（決定係数）が 0.58 というのは、このモデルが住宅価格のばらつきの 58% を説明できていることを意味します。R²の値は1に近いほど良いモデルで、0.7以上であれば良好とされることが多いですが、今回の 0.58 ではやや説明力が不足している可能性があります。

結果の可視化

では、実測値と予測値の関係を散布図で見てみましょう。

plt.scatter(y_test, y_pred, alpha=0.5)
plt.xlabel("住宅価格の実測値")
plt.ylabel("住宅価格の予測値")
plt.title("実測値と予測値の関係")
plt.show()

コードの解説

scatter(y_test, y_pred) で実際の価格と予測値を比較
完璧な予測なら、点が直線的に並ぶはず

結果はこんな感じです。

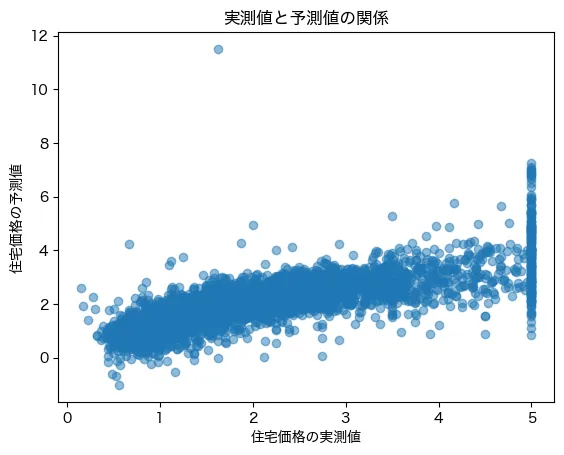
実データでは住宅価格は５を上限に置き換えられている一方、予測値は５以上の値も予測しているため、右端のデータの分布が歪な形状になっています。それ以外は概ね、実際の価格が上がるにつれ、予測値も上がっており大まかな関係性はモデルで説明しているようですね！

具体的に実測値と予測値の関係を相関係数で測定してみましょう。

# y_test, y_predの相関係数
correlation = np.corrcoef(y_test, y_pred)[0, 1]
print(f"相関係数: {correlation:.2f}")

コードのnp.corrcoef(y_test, y_pred)[0, 1]でy_testとy_predのデータの相関関係を計算しています。アウトプットはこんな感じです。

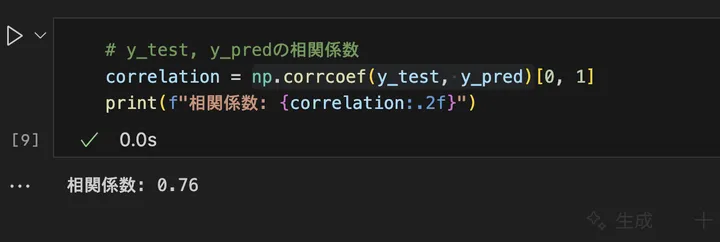
相関係数が0.76なので強い相関（xの直線的な増加に対して、yが直線的に増加する関係）が見られます。

相関係数については以下にも詳しく書いてあるので、よかったら見てください。

あわせて読みたい

データ分析で利用される統計についてみなさん、こんにちは。デジタルボーイです。今回はデータ分析で利用される統計や統計的手法について解説したいと思います。記事を書いた人デジタルボーイです。デー…

あわせて読みたい

データ分析におけるデータの集計みなさん、こんにちは、デジタルボーイです。今回は、データ分析におけるデータの集計について解説したいと思います。記事を書いた人デジタルボーイです。データサイ…

モデルの解釈

続いて、構築した重回帰モデルの中身を見ていきましょう。

# 切片（Intercept）を出力
print(f"Intercept (切片): {model.intercept_}")

# 各変数の回帰係数を出力
coefficients = pd.DataFrame({"Feature": X.columns, "Coefficient": model.coef_})
print(coefficients)

コード解説

model.intercept_ は 回帰式の切片 を表す。
model.coef_ は 各説明変数の回帰係数（影響度） を示す。 pd.DataFrame() を使って、特徴量の名前（X.columns）と対応する回帰係数を一覧化し、見やすく整理。
print(coefficients) で、どの変数が住宅価格にどの程度影響を与えるかを確認できる。

実際の結果はこんな感じでした。

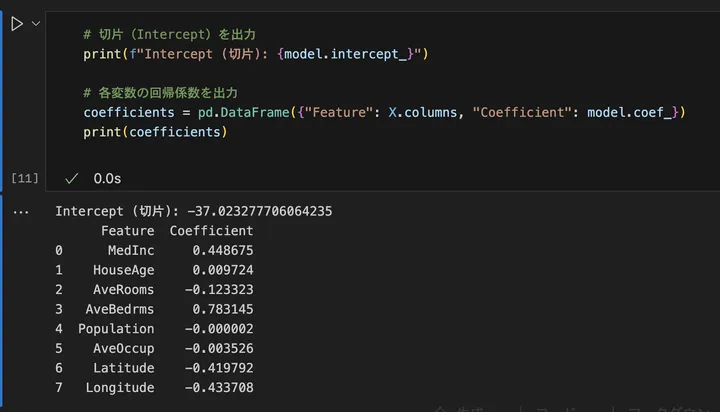
内容は以下のように解釈します。

切片（Intercept）
model.intercept_ の値は -37.02となっています。これは、すべての説明変数が 0 のときの住宅価格を示します。まあ、実際には意味のある値ではないことが多いです。
回帰係数（Coefficient）
model.coef_ の値は、それぞれの特徴量が価格に与える影響を示しています。例えば、MedInc（世帯の中央値所得） の係数が 0.448675 なら、世帯所得が1単位増加すると住宅価格が約0.44上昇する ことを意味します。逆に、Longitude（経度） の係数が -0.433708 なら、経度が1単位増加すると価格が約0.43下がる ことを示します。