こんにちは、デジタルボーイです。今回は僕自身が実務でやっている予測精度を上げるための取り組みについて手順を解説したいと思います。

デジタルボーイです。
データサイエンス歴20年以上のおっさんです。中小企業診断士として、データサイエンス、WEBマーケティング、SEOに関するデータ分析、コンサルティングの仕事をしています。自己紹介の詳細はコチラ
予測モデルの精度を上げるための手順
予測精度を向上させるために、個人的に重要だと感じている手順は以下です。
- データ前処理:欠損値や外れ値の処理
- エンジニアリング:予測に有用な変数を選定し、新たな変数を設計します。
- 特徴量選択:必要な予測モデルに絞りこみ、過学習を防ぎます。
- モデルの選定と学習:複数のアルゴリズムをホールドアウト法やクロスバリデーションで評価し比較します。
これらのステップを体系的に実施することで、予測モデルのパフォーマンスを最大化することが可能です。
精度向上に使われる代表的なモデル
実務や分析の現場では、さまざまな予測モデルが使われています。以下は僕の実務での経験に基づいた予測モデルへの所感です。
予測だけでなく、説明が重要な場合と外挿が必要な場合
コンペだととにかく予測精度を上げることが第一の目的ですが、実務上では予測精度を追い求めるだけではクライアントが納得しないケースも多々あります。どんなに素晴らしい予測モデルを構築しても、クライアントの肌感覚や知見と合致しなければ「へー」というだけで、終わってしまう場合も多々あります。そのようなケースで力を発揮する予測モデルが、回帰分析や重回帰分析になります。これらはシンプルで解釈性が高く、非データサイエンティストにもとっつきやすいという利点があります。また、予測だけでなく、そのデータ間の関連を仮説に基づいて説明するような場合にもこれらのモデルは使いやすいです。あと、予測モデル使ってエクセルでデータを入力しながら予測値をさくっとシミュレーションする(これを「外挿」と言います)にも、回帰分析や重回帰分析はとても使いやすいです。
もちろん、リッジ回帰やラッソ回帰なども基本的なモデルは重回帰と同じで、モデルに正則化項が入っているだけなので、重回帰の利点をそこなうことなしで、多重共線性などを回避できる便利なモデルといえます。
これらのモデルについては以下に詳しく解説してあるのでよかったら参考にしてください。



分類タスクで、予測に加えてわかりやすさが重要な場合
先ほどの重回帰は回帰タスクでわかりやすさに重点をおいたケースで利用しますが、同じような目的で分類タスクでクライアントへの説明のわかりやすさを重視した業務では、ロジスティック回帰や判別分析、決定木をよく使います。
これらのモデルは、シンプルな数式で「どの特徴が結果にどう影響しているか」を明確に示せるため、モデルの中身をクライアントに説明しやすいという利点があります。
特にロジスティック回帰は、プレゼンで「Aになる可能性は◯%」と確率で示せるため、歯切れが良くて重宝しています。
判別分析も、グループ間の差を軸に判断するため、2次元の散布図でグルーピングの様子をプロットできると言う利点から、ビジネスの意思決定において納得感を得やすいモデルといえます。
決定木はなんといってもツリー図のわかりやすさ、インパクト、納得性という点で実務では抜群に使いやすいモデルです。
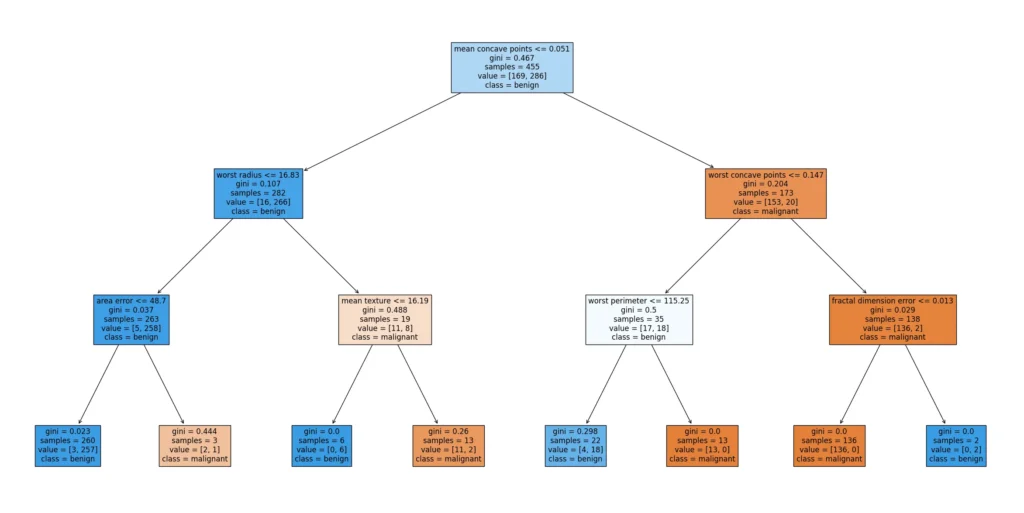
個人的にはわかりやすさを重視する分類タスクで、2値分類だったら決定木かロジスティック、3値以上だったら決定木か判別分析を使うイメージです。これらモデルについては以下に解説をしています。



とにかく予測精度が重要な場合
予測精度が重要な場合は、基本的には複数のモデルを構築しながらモデル選定を行い、もっとも精度の高いモデルを採用するという流れになります。
k近傍法(k-NN)は直感的かつシンプルな手法で、学習フェーズが不要な点が特徴です。ただし外れ値などのの影響を受けやすいという側面もあります。たまにかなりいい精度を出すこともありなかなかどうして侮れないモデルといえます。ランダムフォレストは多数の決定木を組み合わせることで、予測精度を高めるモデルであり安定して良い精度を発揮するモデルという印象です。


同じく、精度が高いと言われているモデルとしてサポートベクターマシン(SVM)と言うのがありますが、僕自身はビジネス場面では、最終的な報告会でこのモデルを採用し報告すると言うことはほぼありません。というのも、このモデルを非データサイエンティストに説明するのが、正直、めんどくさいのと、めんどくささの割に後述のLightGBMといったモデルに比べて特別、予測精度も高いことがあまりなく、他のモデルに比べて利点があまり見当たらないからです。SVMについてはこちらにも解説してあります。

そして、なんといっても予測精度を上げたい場合に抜群に使いやすいモデルがLightGBMになります。このモデルはブースティング型のモデルで、決定木を連結させながら予測の誤差を小さくしていくモデルです。スピードと精度のバランスに優れています。特に大規模データや高次元データにおいては、その高速な学習性能と優れた予測精度から、実務での利用が急速に広がっています。LightGBMについてはこちらに詳しく書いてあるので、参考にしてください。

予測精度向上の対策1:欠損値と外れ値の対処
欠損値と外れ値は、予測モデルの精度に大きな影響を与えるため、慎重に処理する必要があります。
欠損値の対処
欠損値は、データの一部が記録されていない状態を指します。適切に処理しないと、学習アルゴリズムの性能が著しく低下します。最も基本的な方法としては、平均値や中央値、最頻値などによる単純補完があります。
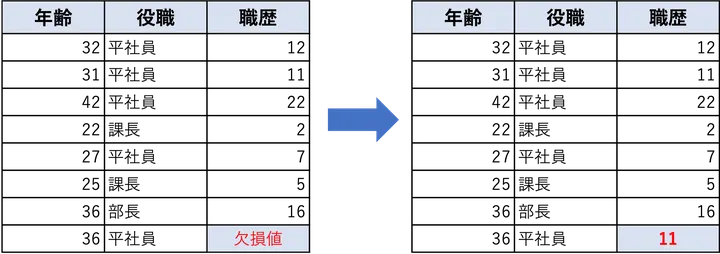
外れ値の対処
外れ値は、他のデータと比べて著しく異なる値のことを指します。これを放置すると、モデルが誤ったパターンを学習してしまう可能性があります。処理方法としては、データ量が十分にある場合には外れ値を削除するのが有効ですが、小規模なデータセットでは慎重に対応すべきです。削除が難しい場合は、中央値や近傍の値での置換が有効です。
欠損値と外れ値の対処法については以下に詳しく解説してあります。

予測精度向上の対策2:特徴量エンジニアリング
特徴量エンジニアリング(Feature Engineering)は、既存のデータから新しい特徴量を作成したり、既存の変数を変換・加工することで、モデルに入力する情報を増やすためのプロセスです。というのも、一般的にはモデルに与える情報が多い方が予測精度は高まるからです。とはいっても、どんどん情報を与えればいいかと言うとそうではなく、ある一定程度で頭打ちになり、さらに予測精度は悪化する方向に進みます。
数値変数に対しては、スケーリングという処理をすることが多いです。例えば、建設関連のデータを分析する場合、鉄筋はt-kgの単位、ガラスはkgの単位、コンクリートはm3の単位と、データのレンジがバラバラだったりします。このようなレンジがバラバラなデータをモデルに入れると、予測精度が落ちてしまう原因になりえます。そのため、スケールやレンジをある程度揃えるという目的から、標準化(Zスコア)や0〜1の変換を行います。
以下は年齢に対して、平均を0、標準偏差を1に標準化変換した例です。
| 年齢 | 年齢_標準化 |
|---|---|
| 18 | -1.167 |
| 25 | -0.702 |
| 30 | -0.371 |
| 45 | 0.623 |
| 60 | 1.6179 |
また、売上やアクセス数など分布が偏っている変数には、対数変換や平方根変換を施すことで、分布を正規分布に近づけ、学習効率の改善が期待できます。さらに、連続値を一定の区間に分けてカテゴリ化するビニング(離散化)を行えば、非線形な関係性を捉えやすくなるケースもあります。
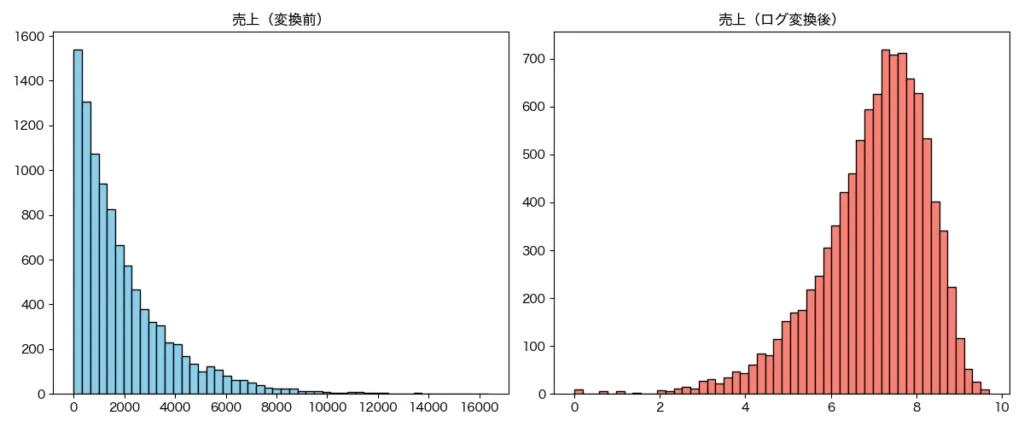
カテゴリ変数に関しては、One-Hotエンコーディングなどの処置があります。これは、各カテゴリごとに新たなフラグ変数を作る手法で、特に線形モデルとの相性が良いです。以下は天気という列をOne hotエンコーディングした例です。
| 天気 | 曇 | 雨 | 晴 |
|---|---|---|---|
| 晴 | 0 | 0 | 1 |
| 曇 | 1 | 0 | 0 |
| 雨 | 0 | 1 | 0 |
| 晴 | 0 | 0 | 1 |
また、さらに高度な手法としては、各カテゴリの目的変数の平均値を特徴量として取り入れるターゲットエンコーディングがあります。ただ、この手法は情報リークを起こすリスクがあるため、扱い方に注意が必要です。また、ツリー系モデルでは、カテゴリを整数に変換するラベルエンコーディングが使われることもありますが、順序性があると誤解されるリスクがあるため注意が必要です。
複数の特徴量を組み合わせることで、モデルに対してより意味のある構造を明示的に与えることもできます。たとえば、単価と購入数を掛け合わせて売上金額の特徴量を作成するなど、掛け算・割り算・差分といった演算を活用します。
| 単価 | 数量 | 売上金額 | 単価差 | 数量比 |
|---|---|---|---|---|
| 100 | 1 | 100 | nan | nan |
| 150 | 2 | 300 | 50 | 2 |
| 200 | 3 | 600 | 50 | 1.5 |
| 250 | 4 | 1000 | 50 | 1.33333 |
| 300 | 5 | 1500 | 50 | 1.25 |
時系列データでは、年月日を単に数値で扱うのではなく、年・月・日・曜日・時間帯などに分解することで周期性や季節性を捉えることができます。さらに、過去の値を表すラグ特徴量や、一定期間の移動平均、傾向スコアといった統計量を追加することで、時系列の文脈をモデルに与えることが可能です。
| 注文日 | 曜日 | 月 | 四半期 | 週末フラグ |
|---|---|---|---|---|
| 2024-04-01 | 月曜 | 4 | 2 | False |
| 2024-04-06 | 日曜 | 4 | 2 | True |
| 2024-05-15 | 水曜 | 5 | 2 | False |
| 2024-06-22 | 土曜 | 6 | 2 | True |
| 2024-07-07 | 日曜 | 7 | 3 | True |
テキストデータにおいては、BoW(Bag of Words)やTF-IDFのような頻度ベースのベクトル化手法がよく用いられます。より意味を捉えたい場合には、Word2VecやBERTなどの埋め込み表現を活用することで、単語や文の意味的な類似性を特徴として抽出できます。
| レビュー | 文字数 | 単語数 | 感嘆符数 |
|---|---|---|---|
| とても美味しかった!また行きたいです。 | 19 | 1 | 1 |
| 味は普通。接客が少し残念でした。 | 16 | 1 | 0 |
| 量が多くて満足。コスパ最高! | 14 | 1 | 1 |
| 期待外れ。もう行かないと思います。 | 17 | 1 | 0 |
| 雰囲気が良くてゆったりできました。 | 17 | 1 | 0 |
特徴量エンジニアリングについては以下に詳しく解説してあります。

予測精度向上の対策3:特徴量選択
続いて特徴量選択(Feature Selection)です。これはある意味、特徴量エンジニアリングの反対の作業といえます。ここでは、ある基準を元に、予測に効く特徴量/説明変数を残しつつ、不要またはノイズとなる変数を排除することです。特に予測精度向上という文脈では、過学習の防止という意味が大きいと思います。僕個人としては、特徴量量選択は、特徴量エンジニアリングで目一杯つくった特徴量をサクッと足切りする作業、というイメージで実務をやっています。
特に僕自身がよく使う手法は以下の通りです。
分散で足切りする
分散で足切りする方法は、まずほとんど値が変化しない(=分散が小さい)特徴量を除外するシンプルな手法です。変化がほぼない特徴量は、ターゲットの予測に寄与しにくいため、あらかじめ排除しておくことで計算効率も上がります。
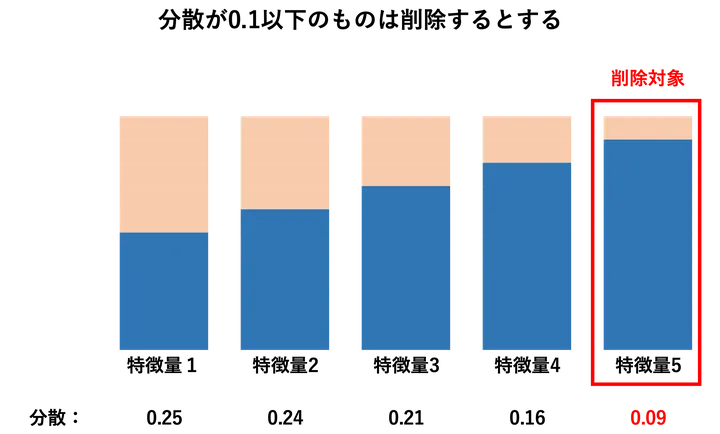
特に初期段階での次の選択ステップを軽くする目的でよく使っています。この方法は、モデルに依存しない前処理的な位置づけで、特徴量のスクリーニングに非常に有効です。
F値で足切りする
F値で足切りする方法は、各特徴量と目的変数との関連性を統計的に評価し、有意な特徴量のみを選ぶ方法です。具体的には、回帰タスクでは分散分析(ANOVA)に基づいたF検定、分類タスクではクラス間の分離度に基づくF分類統計量を用います。これにより、「目的変数に対して強い影響を持つ特徴量」を機械的にスクリーニングできます。モデルに依存せず、かつ高速に計算できるため、前処理段階でのフィルタリングに便利です。特に多次元のデータセットでは、まずこの手法で絞り込むことが多いです。
モデルの特徴量で足切する
モデルの特徴量で足切りする方法は、機械学習モデルの学習結果から得られる特徴量の重要度(Feature Importance)をもとに選択する手法です。たとえばランダムフォレストや勾配ブースティング(LightGBMなど)を用いると、各特徴量がどれだけ予測に貢献したかが数値化されます。これを基準に、一定の重要度を下回る特徴量を除外します。この手法は、実際にモデルにとって「効いたかどうか」を基準にしているため、より実践的な特徴量選択が可能です。精度向上と過学習の抑制を両立できるのが強みです。
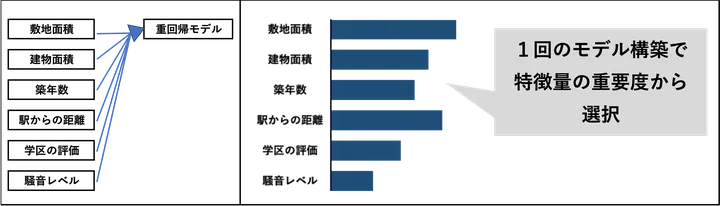
特徴量選択については以下に詳しく解説しているので、よかったら見てください。

予測精度向上の対策4:モデル選定と評価方法の工夫
最後にモデル選定です。モデル選定の技術をしっかりと身につけることで、多くのモデルを構築し、その中から優秀なモデルを選択することができるため、予測タスクでは非常に大切な技術といえます。
僕自身は、分析プロジェクトの初期段階では、解釈性が高くシンプルなモデルを用いてベースラインを作成し、その後、より複雑で精度の高いモデルに発展させるようにしています。特にベースラインではお客さんに中間報告を入れ、変数や予測の方針などを検証できるようにしています。
モデルを評価するためのデータ分割方法としては、十分にデータ件数が多い場合、ホールドアウト法を使うことがおおいです。ホールドアウト法とは、データセットを訓練用、検証用、テスト用に分けてモデルの汎化性能を確認する方法です。

一方で、データ量が限られている場合や評価の安定性を重視する場合には、クロスバリデーション(CV)が有効です。特にk分割交差検証では、全データを学習・評価にバランスよく活用できるため、過学習のリスクを抑えつつ精度の信頼性を高めることが可能です。

時系列データの場合は、通常のk-foldではなく、時間の流れを意識した時系列CVを採用することで、将来予測に近い評価が可能になります。
評価指標についても、目的に応じた選択が求められます。回帰モデルではRMSE(平均二乗誤差の平方根)やMAE(平均絶対誤差)、R²スコア(決定係数)などが使われます。分類モデルでは、Accuracy(正解率)に加えて、Precision(適合率)、Recall(再現率)、F1スコア、AUCなど、モデルの目的やデータのバランスに応じて指標を使い分ける必要があります。特に不均衡なクラス分布を持つタスクでは、Accuracyだけでの判断は誤解を招くため、F1スコアやAUCが重視されます。
例えば、ホールドアウトを行った際の複数モデルの予測値と実測値の関係をプロットしたものが以下となります。横軸は実測値、縦軸は予測値、青い点は学習データ、赤い点は検証データのプロットです。
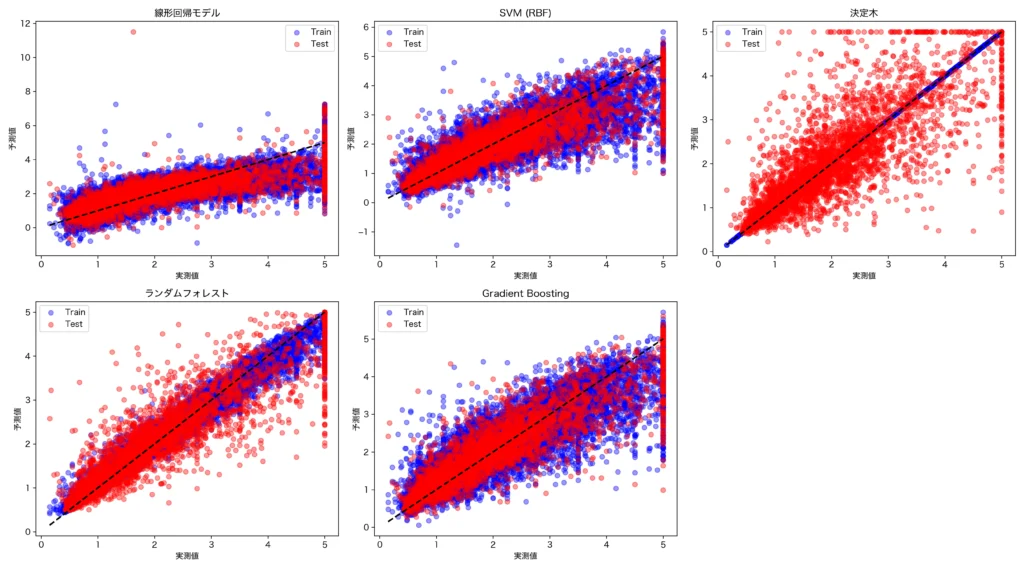
右上は決定木によるプロットですが、青色の点は直線上に綺麗に並んでありほぼ100%学習できていることがわかります。しかし、青い点は直線上から離れてかなりばらついています。これは典型的な過学習のパターンといえます。このように、複数のモデルもホールドアウトやクロスバリデーションを行うことで、学習データだけでなく、将来の未知のデータへの予測も考慮し、最適なモデルの選定を行うことが可能となります。
モデル選定とホールドアウト、クロスバリデーションについては以下に詳しく解説してあります。

おわりに
以上、予測精度を上げるための取り組みについてでした!ここで解説した内容を実践していただき、予測精度の向上にお役立ちいただけると幸いです。
