pythonによる判別分析入門

2025年3月13日

こんにちは、デジタルボーイです。今回は判別分析について、Pythonとscikit-learnを使い、解説したいと思います！

記事を書いた人

デジタルボーイです。
データサイエンス歴20年以上のおっさんです。中小企業診断士として、データサイエンス、WEBマーケティング、SEOに関するデータ分析、コンサルティングの仕事をしています。自己紹介の詳細はコチラ

線形判別分析（Linear Discriminant Analysis, LDA）とは

線形判別分析（LDA） は、データを2つ以上のクラスに分類するための教師あり学習の手法です。特に 2値分類 においては、2つのクラスを分離するための線形の境界（判別面） を見つけることを目的とします。

LDA は 「2つのクラスを最もよく分離する直線（または平面）」を求める ことで、分類を行います。具体的には、各クラスの平均値（重心） と データの分布（共分散行列） を考慮して、最適な分離線を決定します。

例えば２変数で判別分析を実行した場合のクラスを識別している様子です。

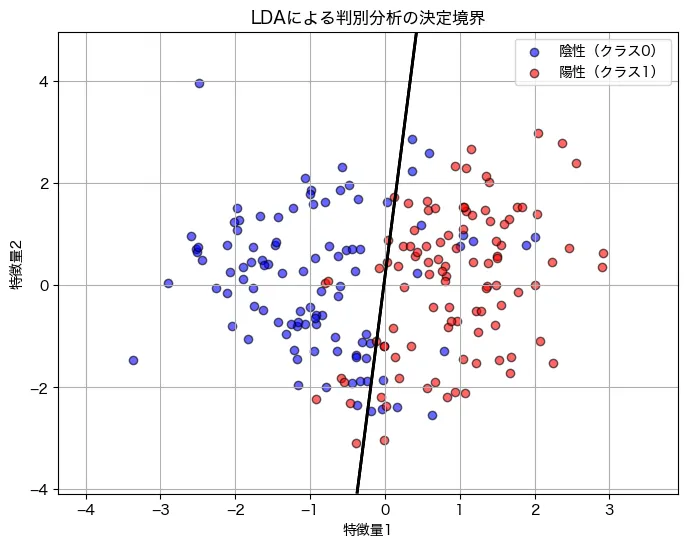
LDAの応用場面

LDAは、クラスごとにデータが正規分布に近い場合 に特に有効です。以下のような実際の分類問題で利用されています。

医療診断
- 例: 腫瘍が「良性」か「悪性」かを分類（がん診断）
マーケティング
- 例: 顧客が「購入する」か「購入しない」かを予測
金融
- 例: クレジットカードの不正使用を検知
顔認識
- 例: 画像データを特徴空間に投影して分類

必要なライブラリのインポート

LDAを実装するには、以下のライブラリが必要です。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report

コードの解説

numpy と pandas はデータ処理のために使用
matplotlib.pyplot は可視化に使用
train_test_split はデータを学習用とテスト用に分割
StandardScaler は特徴量のスケーリングを行う
LogisticRegression はロジスティック回帰モデル
accuracy_score などはモデル評価のために使用

もし、上記のライブラリをインストールしていない場合は、 pip install しましょう。

pip install numpy pandas matplotlib scikit-learn

pipを使ったインストール方法はこちらになります。

データ概要の確認

今回は、scikit-learn に含まれる 乳がん診断データセット（breast_cancer） を使用します。このデータセットは、腫瘍が「良性（0）」か「悪性（1）」かを分類するタスクに適しています。

from sklearn.datasets import load_breast_cancer

# データの読み込み
data = load_breast_cancer()
X = data.data
y = data.target

# データの概要を表示
print("特徴量の数:", X.shape[1])
print("データのサンプル数:", X.shape[0])
print("クラスの分布:", np.bincount(y))
print("特徴量の名前:", data.feature_names)

コードの解説

load_breast_cancer() で乳がんデータセットをロード
X.shape[1] で特徴量の数を取得
X.shape[0] でデータのサンプル数を取得
np.bincount(y) でクラスごとのデータ数を確認
data.feature_names で特徴量の名前を取得

結果はこうでした。

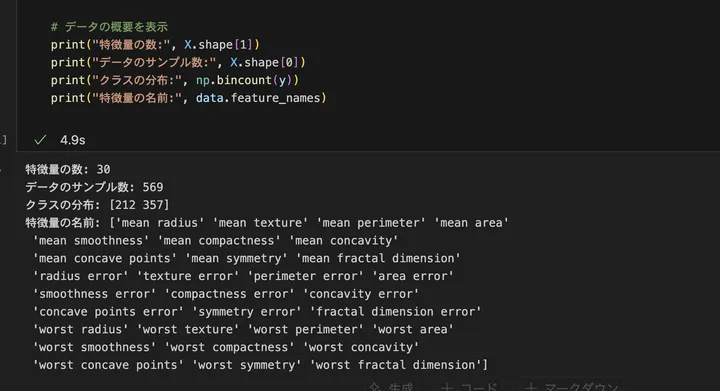
特徴量は３０、サンプル数は５６９、ターゲットは陰性：２１２件、陽性：３５７件です。

分析の目的とゴール

今回の分析の目的は、乳がん診断データセットを用いて、腫瘍が良性か悪性かを線形判別分析（LDA）で分類することです。

このモデルを構築することで、以下のゴールを達成します。

医療診断の支援
LDAモデルを活用し、新しい患者データが良性か悪性かを予測する
モデルの精度評価
予測結果を評価し、分類の正確性を確認する
重要な特徴量の把握
どの特徴が分類に影響を与えているかを明らかにする

モデルの実装

LDAモデルを構築し、乳がんデータセットを学習させます。

# データの準備
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# データの標準化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# LDAモデルの学習
model = LinearDiscriminantAnalysis()
model.fit(X_train_scaled, y_train)

# 予測
y_pred = model.predict(X_test_scaled)
y_pred_proba = model.predict_proba(X_test_scaled)[:, 1]  # 確率スコア

コードの解説

train_test_split() を使い、データを 80%を学習用、20%をテスト用 に分割
StandardScaler() で特徴量のスケーリングを行い、モデルの精度向上を図る
LinearDiscriminantAnalysis() を用いて LDA モデルを作成し、fit() を実行
predict() でクラスラベル（0または1）を予測
predict_proba() でクラス1（悪性）になる確率を取得

モデルの評価

LDAモデルの評価には、回帰モデルの評価指標である MSE（平均二乗誤差）, RMSE（平方根平均二乗誤差）, R²（決定係数） を計算します。また、分類タスクのため、正解率や混同行列も確認します。

from sklearn.metrics import mean_squared_error, r2_score, accuracy_score, confusion_matrix, classification_report

# MSE, RMSE, R² の計算
mse = mean_squared_error(y_test, y_pred_proba)
rmse = np.sqrt(mse)
r2 = r2_score(y_test, y_pred_proba)

# 正解率、混同行列、詳細レポート
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
report = classification_report(y_test, y_pred)

# 結果の出力
print("MSE:", mse)
print("RMSE:", rmse)
print("R²:", r2)
print("正解率:", accuracy)
print("混同行列:\n", conf_matrix)
print("詳細レポート:\n", report)

結果はこうでした。

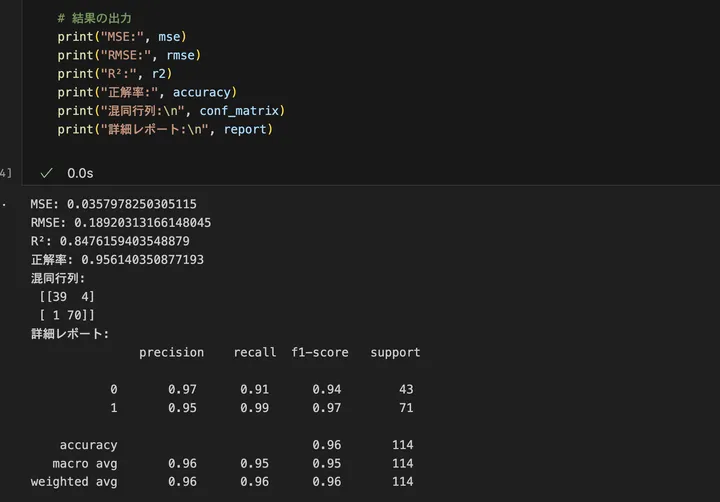
では、具体的に推定した数値から今回のモデルを解釈してみましょう。

今回推定したモデルの誤差指標（MSE, RMSE, R²）からの解釈

MSE（平均二乗誤差）: 0.0358
モデルの予測確率と実際のラベルとの誤差の二乗平均が 0.0358 という小さい値になっています。
→ モデルの予測はかなり精度が高く、実際のラベルとほぼ一致している と考えられます。
RMSE（平方根平均二乗誤差）: 0.1892
平均二乗誤差の平方根を取ることで、誤差の大きさを直感的に理解しやすくした指標。
→ モデルの出力確率と実際のクラスとの差は、平均して約0.19（19%）程度のズレしかない ため、十分に良い予測精度と言えます。
R²（決定係数）: 0.8476
決定係数は、モデルがデータのパターンをどれだけうまく説明できているかを示す指標で、1に近いほど良いモデル となります。
→ 今回の R² = 0.8476 は、モデルが約85%のデータの変動を説明できていることを示しており、LDAの判別精度が高いことがわかる。

分類性能の評価（正解率, 混同行列, Precision-Recall）

○正解率（Accuracy）: 95.6%

全体の95.6%のデータを正しく分類できた ことを示しています。
→ LDAは、今回のデータに対して非常に高い分類精度を持っている。

○混同行列

実際\予測	予測 0（良性）	予測 1（悪性）
実際 0（良性）	39（TN）	4（FP）
実際 1（悪性）	1（FN）	70（TP）

○混同行列の解釈

39件（TN） → 実際に良性で、正しく良性と予測
70件（TP） → 実際に悪性で、正しく悪性と予測
4件（FP） → 実際は良性なのに、誤って悪性と予測（偽陽性）
1件（FN） → 実際は悪性なのに、誤って良性と予測（偽陰性）

○偽陽性（FP）が4件と、偽陰性（FN）が1件発生しているが、FNが極めて少ないのは重要

悪性なのに良性と誤診（FN）が 1件しかない のは、医療診断の観点から見ても望ましい傾向。
良性なのに悪性と誤診（FP）が 4件発生 しているが、誤診されたケースで追加検査を行うことで実害を防ぐことは可能。

適合率（Precision）、再現率（Recall）、F1スコア

○クラス0（良性）

Precision（適合率）: 97%
- 良性と予測したうち、実際に良性であった割合
- 高い値なので、良性と予測したものはほぼ正しい
Recall（再現率）: 91%
- 実際に良性のデータのうち、正しく良性と予測できた割合
- やや低め（91%）なので、一部の良性が誤って悪性と予測されている

○クラス1（悪性）

Precision（適合率）: 95%
- 悪性と予測したうち、実際に悪性であった割合
- ほぼ正しい悪性判定ができている
Recall（再現率）: 99%
- 実際に悪性のデータのうち、正しく悪性と予測できた割合
- ほぼ100%に近い（99%）ため、悪性を見逃す確率は極めて低い

→ 悪性の検出性能（Recall 99%）が非常に高いため、LDAモデルは悪性を見逃しにくい。

今回の線形判別分析（LDA）モデルの評価結果から、予測確率と実際のラベルがほぼ一致しており、高い精度の分類ができていることがわかります。MSEが0.0358、RMSEが0.1892、R²が0.8476という数値は、モデルの誤差が小さく、データのパターンを適切に捉えていることを示しています。特に、正解率は95.6%と非常に高く、悪性腫瘍の検出能力を示す再現率（Recall）が99%に達している点からも、悪性を見逃さない優れた診断補助ツールになり得ることが確認できます。一方で、偽陽性（FP）が4件あり、良性腫瘍の一部が誤って悪性と判断される可能性はあるものの、追加の検査を行うことでこの問題には十分に対応可能です。LDAはこのデータセットに対して、良性と悪性の特徴を適切に学習し、高い判別精度を持つモデルを構築できたといえるでしょう！

特徴量の重要度

続いて、特徴量の重要度についてみていきましょう。以下のコードを打ち込んでみてください。

# 日本語フォント設定（Mac用）
plt.rcParams["font.family"] = "Hiragino sans"

# 説明変数の重要度（LDAの係数）
coefficients = model.coef_[0]  # 各特徴量の重み
feature_names = data.feature_names

# 影響の大きい順に並び替え
sorted_indices = np.argsort(np.abs(coefficients))[::-1]
sorted_features = np.array(feature_names)[sorted_indices]
sorted_coefficients = coefficients[sorted_indices]

plt.figure(figsize=(10, 6))
plt.barh(sorted_features[:10], sorted_coefficients[:10], color="steelblue")  # 上位10特徴量のみ表示
plt.xlabel("回帰係数の値")
plt.ylabel("特徴量")
plt.title("LDAの説明変数の重要度")
plt.gca().invert_yaxis()
plt.show()

コードの解説

plt.rcParams["font.family"] = "Hiragino sans" は、グラフ内のフォントを設定する。Mac用の日本語フォント「Hiragino Sans」を指定しており、Windows環境では plt.rcParams["font.family"] = "Meiryo"] などに変更する必要がある。
coefficients = model.coef_[0] は、LDAモデルの係数（重み）を取得する。各特徴量が分類に与える影響の大きさを表す。
feature_names = data.feature_names は、乳がんデータセットの特徴量名を取得する。各特徴量がどのような物理的な意味を持つかを確認するために使用する。
sorted_indices = np.argsort(np.abs(coefficients))[::-1] は、係数の絶対値の大きい順にインデックスを取得する。np.argsort() は昇順に並べるため、[::-1] で降順に並び替えている。影響の大きい特徴量を上位に持ってくるための処理。
sorted_features = np.array(feature_names)[sorted_indices] は、ソート済みの特徴量名を取得する。係数の大きさに応じた特徴量の重要度を確認するために使用。
sorted_coefficients = coefficients[sorted_indices] は、影響の大きい順に並べ替えた係数の値を取得する。どの特徴量が正の影響を持つか、負の影響を持つかを確認できる。
plt.figure(figsize=(10, 6)) は、グラフのサイズを指定する。幅10インチ、高さ6インチのグラフを作成する。
plt.barh(sorted_features[:10], sorted_coefficients[:10], color="steelblue") は、上位10個の特徴量を横棒グラフで表示する。color="steelblue" で棒の色を設定。
plt.xlabel("回帰係数の値") は、x軸のラベルを「回帰係数の値」とする。各特徴量の重みがどれくらいの影響を持つかを示す。
plt.ylabel("特徴量") は、y軸のラベルを「特徴量」とする。どの特徴量が重要であるかを明示する。
plt.title("LDAの説明変数の重要度") は、グラフのタイトルを「LDAの説明変数の重要度」とする。モデルがどの変数を重要視しているかを表す。
plt.gca().invert_yaxis() は、y軸の順序を反転する。影響の大きい特徴量を上に表示するために使用。
plt.show() は、グラフを表示する。

結果はこうでした。

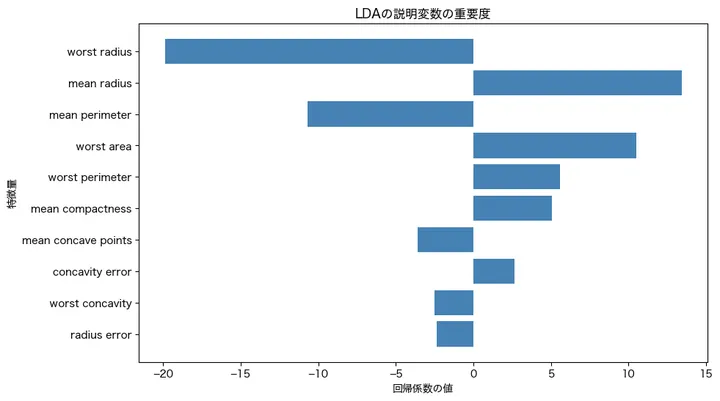
では、重要度の高い変数を見ていきましょう。今回のモデルで、上から三つ、分類に大きな影響を与えた特徴量は worst radius、mean radius、mean perimeterでした。これらの特徴量の係数の符号と大きさを考慮し、それぞれの影響を解釈してみましょう。

worst radius は -19.88 という大きな負の値を持っており、腫瘍の「最大半径」が大きいと、良性（0）に分類される傾向が強いことを意味します。つまり、腫瘍の半径が極端に大きい場合、悪性ではなく良性と判断される可能性が高いと考えられます。

mean radius は 13.43 という正の値を持っており、「平均半径」が大きいほど、悪性（1）に分類されやすいことを示しています。これは、腫瘍全体のサイズが比較的大きい場合、悪性の可能性が高くなることを示唆していると考えられます。

mean perimeter は -10.68 の負の値を持っており、「平均周囲長」が大きいと良性（0）に分類される傾向があることを意味します。mean radius の影響とは逆の方向になっていますが、これは腫瘍の形状や成長パターンに関連している可能性があります。

この結果から、悪性の腫瘍は一般的に「半径」「周囲長」が大きく、形状がより不規則である傾向があると考えられます。一方、極端に大きな半径を持つ腫瘍は良性と分類されやすいことも示唆されており、単純にサイズが大きいから悪性というわけではなく、形状の特徴との組み合わせが重要であると考えられます。

まとめ

以上、簡単ですが判別分析について解説してみました！ぜひ、活用してみてください。