pythonによる回帰分析〜ロジスティック回帰モデル

こんにちは、デジタルボーイです。今回は回帰モデルの中の１モデル、ロジスティック回帰モデルについて、Pythonとscikit-learnを使い、解説したいと思います！

ちなみにこれまで、単回帰分析、重回帰分析についても解説しています。ロジスティック回帰モデルはこれらのモデルの応用モデルと言えるので、必要があれば以下の解説を先におさらいしてみてください。

あわせて読みたい

pythonによる回帰分析、初歩の初歩〜単回帰モデル こんにちは、デジタルボーイです。今回は機械学習や統計モデルの初めの一歩とも言える、単回帰分析について、Pythonとscikit-learnを使い、初歩の初歩について解説した…

あわせて読みたい

pythonによる回帰分析〜重回帰モデル入門 こんにちは、デジタルボーイです。前回は機械学習や統計モデルの初めの一歩とも言える、単回帰分析について学習しました。 データ分析を始めたばかりの方にとって、複数…

記事を書いた人

デジタルボーイです。
データサイエンス歴20年以上のおっさんです。中小企業診断士として、データサイエンス、WEBマーケティング、SEOに関するデータ分析、コンサルティングの仕事をしています。自己紹介の詳細はコチラ

ロジスティック回帰分析とは？

ロジスティック回帰（Logistic Regression）は、2値分類問題を解くための代表的な機械学習モデルです。このモデルは、入力データから0または1といった2つのクラスに分類するために使用されます。例えば、以下のような場面で利用されます。

• スパムメール分類（メールがスパムかどうか）
• 顧客の購買予測（特定の商品を購入するかどうか）
• 医療診断（患者が特定の病気にかかっているかどうか）

モデルの直感的な理解

ロジスティック回帰は、入力値 xxx に対して、確率 ppp を出力します。この確率が0.5以上なら「1」、それ未満なら「0」と分類します。数式では以下のように表されます。

$$
p = \frac{1}{1 + e^{-(w x + b)}}
$$

この式により、出力が0から1の間の確率として表現されるため、分類問題に適しています。

ロジスティック回帰の特徴を視覚的に理解するために、データと2値を決定する閾値を示すプロットを見てみましょう。

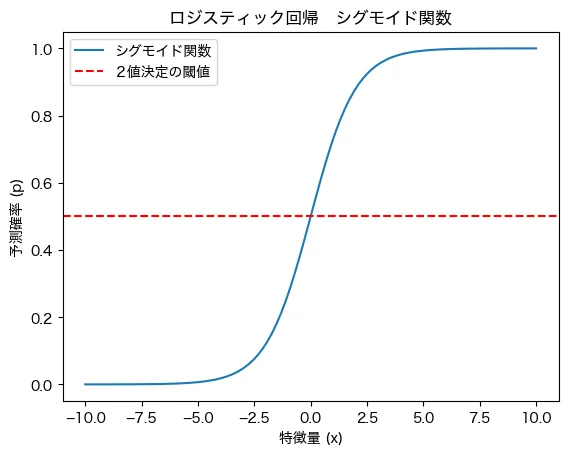
これは特徴量であるxが増加するにつれて、予測値が上がっており、その下限と上限は０〜１となっています。この曲線はロジスティック回帰分析が予測する予測値の曲線で、シグモイド関数と言われています。

また、予測値は連続的な値として算出されますが、そこから２値を割り振るための閾値が赤い点線になります。予測値がこれより上だったら１、そうでなければ０というように割り振る流れになります。

ロジスティック回帰の応用場面

ロジスティック回帰は、多くの実世界の問題で利用されています。例えばこんな感じです。

• マーケティング
  • 顧客が広告をクリックするか（クリック率予測）
  • ユーザーがサブスクリプションを解約するか（解約予測）
• 医療
  • 患者が特定の病気を持っているか（診断補助）
  • 手術成功率の予測
• 金融
  • クレジットカードの不正利用検出
  • ローンの返済遅延リスクの予測
• 製造業
  • 製品が不良品かどうかの分類
  • センサー情報から機械の異常を検知

必要なライブラリのインポート

ラッソ回帰を実装するためには、以下のライブラリが必要です。インストールしていない場合は、先に pip install しましょう。

pip install numpy pandas matplotlib scikit-learn

pipを使ったインストール方法はこちらになります。

あわせて読みたい

pipでpandasをインストールする方法 こんにちは、デジタルボーイです。備忘録がてら、macとLinuxにpipでpandasをインストールするための手順を、まとめておきます。 記事を書いた人 デジタルボーイです。デ…

あわせて読みたい

pipでnumpyをインストールする方法 こんにちは、デジタルボーイです。備忘録がてら、macとLinuxにpipでNumPyをインストールするための手順を、まとめておきます。 記事を書いた人 デジタルボーイです。デ…

あわせて読みたい

pipでscikit-learn(sklearn)をインストールする方法： こんにちは、デジタルボーイです。備忘録がてら、macとLinuxにpipでscikit-learn(sklearn)をインストールするための手順を、まとめておきます。 記事を書いた人 デジタ…

まずは、必要なライブラリをインポートしましょう。

インポートするライブラリは以下の通りです。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report

データ概要の確認

今回は scikit-learn に含まれる 乳がん診断データセット（breast_cancer）を使用します。このデータセットは、腫瘍が良性（0）か悪性（1）かを分類するタスクに適しています。

まずはデータの概要を確認してみましょう。

from sklearn.datasets import load_breast_cancer

# データの読み込み
data = load_breast_cancer()
X = data.data
y = data.target

# データの概要を表示
print("特徴量の数:", X.shape[1])
print("データのサンプル数:", X.shape[0])
print("クラスの分布:", np.bincount(y))
print("特徴量の名前:", data.feature_names)

アウトプットはこんな感じです。

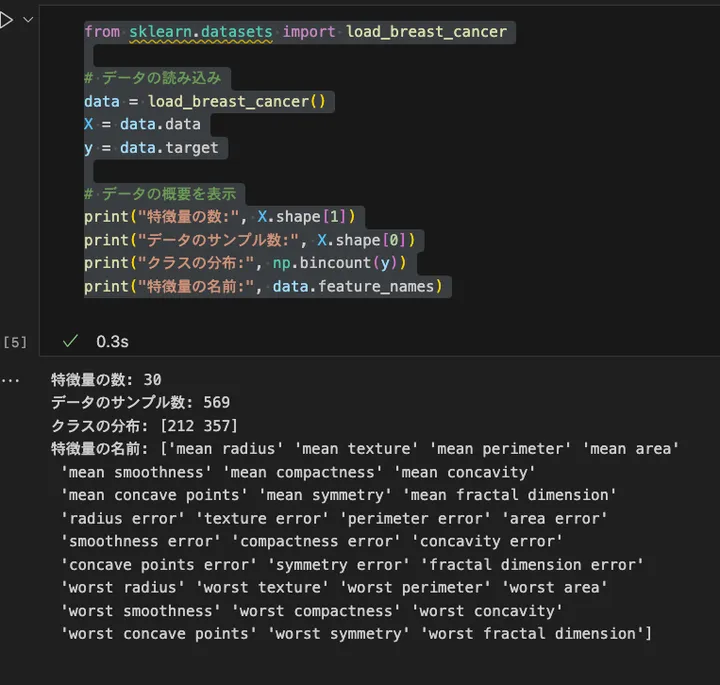
このデータセットには ３0個の特徴量 があり、それぞれが乳がんの発症に関連しています。クラスの分布は、未発症が０（２１２件）、発症が１（３５７件）となっています。

分析の目的とゴール

今回の分析の目的は、乳がん診断データセットを用いて、腫瘍が良性か悪性かをロジスティック回帰モデルで分類することです。

このモデルを構築することで、以下のゴールを達成します。

モデルの実装

ロジスティック回帰モデルを構築し、乳がんデータセットを学習させます。

# データの準備
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# データの標準化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# モデルの学習
model = LogisticRegression()
model.fit(X_train_scaled, y_train)

# 予測
y_pred = model.predict(X_test_scaled)

モデルの評価

ロジスティック回帰モデルの評価には、以下の指標を使用します。

• 正解率 (Accuracy)：正しく分類された割合
• 混同行列 (Confusion Matrix)：分類結果を詳細に確認
• 適合率, 再現率, F1スコア：より詳細な分類評価指標

また、回帰モデルとは異なり、MSE (平均二乗誤差), RMSE (平方根平均二乗誤差), R²乗 (決定係数) は使用しません。代わりに分類問題に適した評価指標を用います。

# モデル評価
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
report = classification_report(y_test, y_pred)

# 結果の出力
print("正解率:", accuracy)
print("混同行列:\n", conf_matrix)
print("詳細レポート:\n", report)

結果はこうでした。

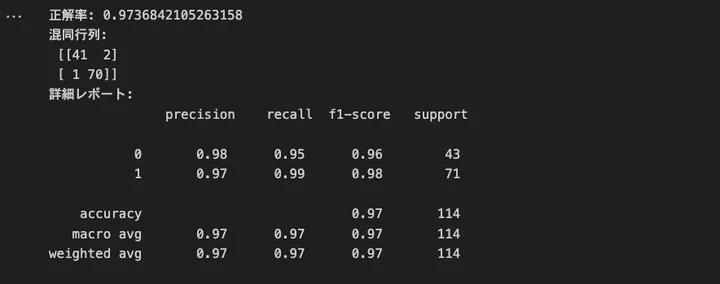
正解率が97.3％とかなりいい感じに予測できていることがわかります。また、　アウトプットにある「混同行列」は、モデルの分類結果を 「実際のクラス」と「予測クラス」 の対応で整理したものです。結果はこんな感じで見ることができます。

混同行列の見方：
---------------
[[TN  FP]
 [FN  TP]]

• TN (True Negative): 実際にネガティブ（クラス0）で、モデルもネガティブと予測した数
• FP (False Positive): 実際はネガティブ（クラス0）だが、モデルが誤ってポジティブと予測した数
• FN (False Negative): 実際はポジティブ（クラス1）だが、モデルが誤ってネガティブと予測した数
• TP (True Positive): 実際にポジティブ（クラス1）で、モデルもポジティブと予測した数

で、今回の混同行列は実際には以下の結果でした。

混同行列：
 [[41  2]
 [ 1 70]]

各値は以下に対応します。

ここから、それぞれの評価指標も計算できます。

• 正解率 (Accuracy)
  • (TP + TN) / 全データ数 = (70 + 41) / (41 + 2 + 1 + 70) = 111 / 114 ≈ 97.37%
• 適合率 (Precision, 陽性的中率)
  • TP / (TP + FP) = 70 / (70 + 2) = 70 / 72 ≈ 97.22%
• 再現率 (Recall, 真陽性率)
  • TP / (TP + FN) = 70 / (70 + 1) = 70 / 71 ≈ 98.59%
• F1スコア (Precision と Recall のバランス指標)
  • 2 * (Precision * Recall) / (Precision + Recall) ≈ 97.90%

つまり、正解率97.37%と高いが、2件の誤分類 (FP) がある。これは、実際にネガティブなのに誤ってポジティブと予測されるケースが発生（例: 「がんではないのにがんと診断」）。また、ポジティブクラスの予測精度が高いつまり、70件中1件しか間違えていない（FN = 1）ということが言えます。

結果をグラフで確認

では、実際の予測状況をグラフでも確認してみましょう。ちょっと長いですが、こんな感じです。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import confusion_matrix

# 日本語フォント設定（Mac用）
plt.rcParams["font.family"] = "Hiragino sans"

# 混同行列の取得
conf_matrix = confusion_matrix(y_test, y_pred)

# 混同行列の値
tn, fp, fn, tp = conf_matrix.ravel()

# 正解・不正解率の計算
total_pos = tp + fn  # 実際のポジティブの総数
total_neg = tn + fp  # 実際のネガティブの総数

pos_correct_rate = tp / total_pos if total_pos > 0 else 0  # ポジティブの正解率
pos_incorrect_rate = fn / total_pos if total_pos > 0 else 0  # ポジティブの不正解率

neg_correct_rate = tn / total_neg if total_neg > 0 else 0  # ネガティブの正解率
neg_incorrect_rate = fp / total_neg if total_neg > 0 else 0  # ネガティブの不正解率

# 構成比の積み上げグラフのデータ
rates = np.array([[pos_correct_rate, pos_incorrect_rate],
                  [neg_correct_rate, neg_incorrect_rate]])

# 実数の積み上げグラフのデータ
counts = np.array([[tp, fn],
                   [tn, fp]])

labels = ["ポジティブ", "ネガティブ"]
categories = ["正解", "不正解"]
colors = ["#1f77b4", "#ff7f0e"]  # 正解（青）・不正解（オレンジ）

# サブプロットの作成
fig, axes = plt.subplots(1, 2, figsize=(12, 6))

# 構成比の積み上げグラフ
axes[0].bar(labels, rates[:, 0], label="正解", color=colors[0])
axes[0].bar(labels, rates[:, 1], bottom=rates[:, 0], label="不正解", color=colors[1])
axes[0].set_ylabel("構成比")
axes[0].set_title("ポジティブ・ネガティブの正解/不正解率（構成比）")
axes[0].legend()

# 実数の積み上げグラフ
axes[1].bar(labels, counts[:, 0], label="正解", color=colors[0])
axes[1].bar(labels, counts[:, 1], bottom=counts[:, 0], label="不正解", color=colors[1])
axes[1].set_ylabel("件数")
axes[1].set_title("ポジティブ・ネガティブの正解/不正解数（実数）")
axes[1].legend()

# グラフの表示
plt.tight_layout()
plt.show()

結果はこんな感じです。

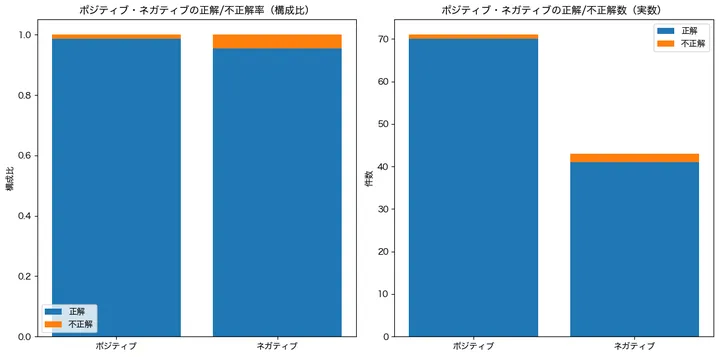
左側は正解と不正解の構成比をポジティブ（陽性）とネガティブ（陰性）ごとにプロットしています。ネガティブの方が不正解の率が高いことが見て取れます。また、右側は実数をプロットしています。実数で見ても、ネガティブ（陰性）の方が不正解のボリュームは多いことが見えますね！

変数の重要度

最後に、ロジスティック回帰の予測にどの特徴量（変数）が効いているのかを見てみましょう。

import matplotlib.pyplot as plt
import numpy as np

# 日本語フォント設定（Mac用）
plt.rcParams["font.family"] = "Hiragino sans"

# モデルの係数取得
coefficients = model.coef_[0]  # ロジスティック回帰の各特徴量の重み
feature_names = data.feature_names  # 特徴量の名前

# 係数の絶対値の大きい順にソート
sorted_indices = np.argsort(np.abs(coefficients))[::-1]
sorted_features = np.array(feature_names)[sorted_indices]
sorted_coefficients = coefficients[sorted_indices]

# プロット
plt.figure(figsize=(10, 6))
plt.barh(sorted_features[:10], sorted_coefficients[:10], color="steelblue")  # 上位10特徴量のみ表示
plt.xlabel("回帰係数の値")
plt.ylabel("特徴量")
plt.title("ロジスティック回帰の説明変数の重要度")
plt.gca().invert_yaxis()  # 上位の特徴量を上にする

# グラフの表示
plt.show()

結果はこうでした。

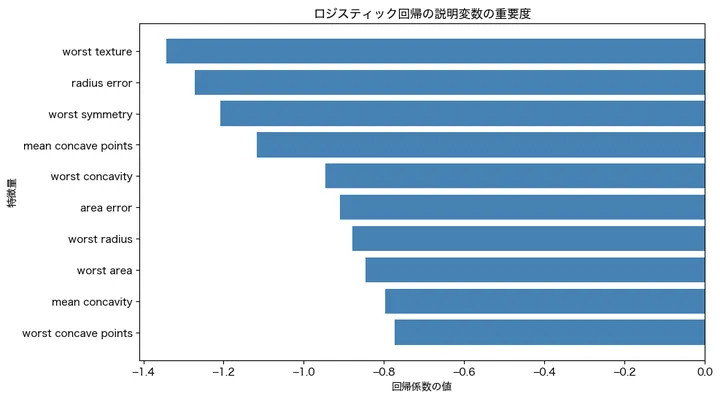
ロジスティック回帰モデルの予測において、worst texture（最も悪いテクスチャ）、radius error（半径の誤差）、worst symmetry（最も悪い対称性）、mean concave points（凹点の平均数）の4つの変数が特に重要でした。

worst textureは、腫瘍の組織の模様の粗さを表し、悪性腫瘍は異常増殖により組織の密度や形状が不均一になりやすいため、この値が高いほど悪性の可能性が高まります。

radius errorは、腫瘍の半径のばらつきを示し、良性の腫瘍が比較的均一な円形であるのに対し、悪性の腫瘍は不規則な形を持つことが多く、半径のばらつきが大きくなるため、この値が大きいほど悪性である可能性が高いと考えられます。

worst symmetryは、腫瘍の対称性の崩れ具合を示し、良性の腫瘍は比較的円形で対称性が高いのに対し、悪性の腫瘍は異常増殖により形が不規則になり左右対称性が失われるため、この値が大きいほど悪性の可能性が高まります。

mean concave pointsは、腫瘍の境界線における「へこみ」の数の平均値を示し、良性の腫瘍は滑らかな境界線を持つのに対し、悪性の腫瘍は不規則な増殖によって境界がギザギザになり、凹点の数が増えるため、この値が大きいほど悪性である可能性が高くなります。

これらの変数はすべて腫瘍の形状や境界の不規則性に関係しており、特に「半径の誤差」「凹点の平均数」「対称性の悪さ」は悪性腫瘍に特徴的なパターンを捉えているため、診断の精度向上に貢献している可能性があります。

まとめ

この分析では、ロジスティック回帰モデルを用いて、乳がんデータセットの腫瘍が良性か悪性かを分類しました。モデルの性能評価には、混同行列を使用し、ポジティブ（悪性）・ネガティブ（良性）それぞれに対する正解率と不正解率を計算しました。可視化として、正解・不正解の構成比を積み上げグラフで示し、分類のバランスを確認しました。また、実際の正解数・不正解数の積み上げグラフを描画し、誤分類の傾向を明確にしました。これにより、モデルがどの程度信頼できるかや、誤分類の影響を直感的に理解できます。結果を活用することで、医療診断の補助や分類モデルの改善に役立てることができます。