こんにちは、デジタルボーイです。今回は予測精度をあげるための欠損値と外れ値の処理テクニックについて、Pythonプログラミングを使いながら解説したいと思います。

デジタルボーイです。
データサイエンス歴20年以上のおっさんです。中小企業診断士として、データサイエンス、WEBマーケティング、SEOに関するデータ分析、コンサルティングの仕事をしています。自己紹介の詳細はコチラ
欠損値と外れ値について
機械学習モデルの精度を高めるため、個人的に一番初めに取り掛からないといけない手順が、この欠損値と外れ値の対応だと思っています。ちなみに、本などではこの欠損値と外れ値の処理のことをまとめて「データの前処理」と言ったりもします。
というのも、欠損値や外れ値は、適切に処理しないとモデルの学習に悪影響を与え、過学習や精度低下の原因になることがあります。しかし、逆にうまく処理することで、モデルの予測精度を大きく向上させることも可能です。
本記事では、欠損値と外れ値の基本的な考え方から、実務で使える処理方法までをわかりやすく解説します。Pythonによる具体的なコード例も交えながら、実際の業務やコンペでも活用できるノウハウを紹介していきます。
欠損値と外れ値が予測精度を下げてしまう例
欠損値と外れ値の処理をする前に、これらが予測にどのように悪影響を与えるのか、見てみましょう。次はpythoでダミーデータを作り、かつ、欠損値と外れ値を意図的に入れたデータです(pythonコードはブログの内容と特に関係ないので、確認しなくてもOKです)。
pythonコードを見る
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
age = np.random.normal(30, 5, 100)
income = age * 15 + np.random.normal(0, 10, 100) + 100 # 緩やかな線形関係
df = pd.DataFrame({'age': age, 'income': income})
# 2. 欠損と外れ値を追加
df.loc[np.random.choice(df.index, 5, replace=False), 'age'] = np.nan # 欠損
df.loc[np.random.choice(df.index, 3, replace=False), 'income'] = np.nan # 欠損
df.loc[0, 'age'] = 90 # 外れ値(年齢)
df.loc[1, 'income'] = 2000 # 外れ値(収入)
# 欠損値の確認
print("▼ 欠損値の数")
print(df.isnull().sum())
# 欠損値の可視化
plt.figure(figsize=(8, 2))
plt.imshow(df.isnull(), aspect='auto', cmap='gray')
plt.title('欠損値の可視化')
plt.xlabel('列名')
plt.ylabel('サンプル')
plt.xticks(ticks=range(len(df.columns)), labels=df.columns)
plt.savefig('missing_value_map.webp', format='webp')
plt.show()
# 外れ値の確認(箱ひげ図で視覚化)
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.boxplot(df['age'].dropna())
plt.title('年齢の箱ひげ図')
plt.subplot(1, 2, 2)
plt.boxplot(df['income'].dropna())
plt.title('収入の箱ひげ図')
plt.tight_layout()
plt.savefig('boxplot.webp', format='webp')
plt.show()
年齢と収入に関するダミーデータを作ってみました。以下は欠損値を可視化した白黒マップです。白い線が欠損値を表しています。

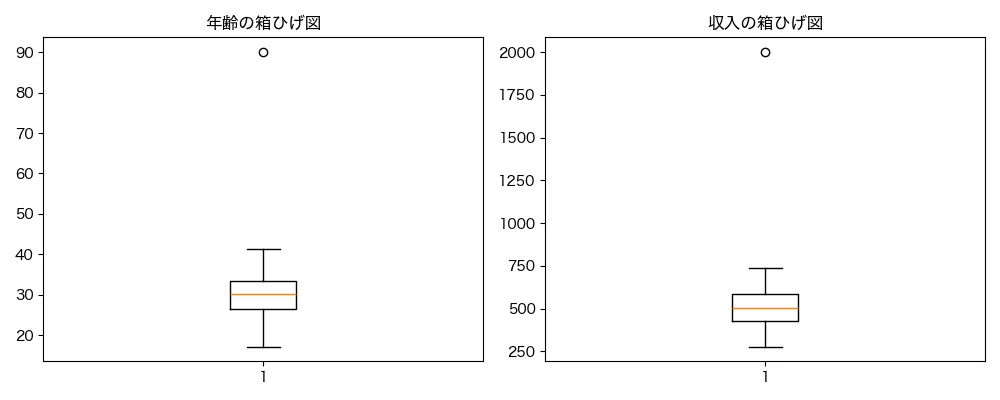
また、以下は年齢と収入のそれぞれの分布を示した箱ひげ図です。グラフの上側に表示された○が外れ値を表しています。
そして、①欠損値と外れ値に処理をしていないデータパターンと②欠損値と外れ値に処理をしたデータパターン(欠損値は中央値で補完し、外れ値は除外)の2パターンで、年齢から収入を予測する回帰モデルを作成した結果(横軸:年齢、縦軸:年収)が以下となります。青色が実際の値、オレンジ色がモデルで予測した値になります。
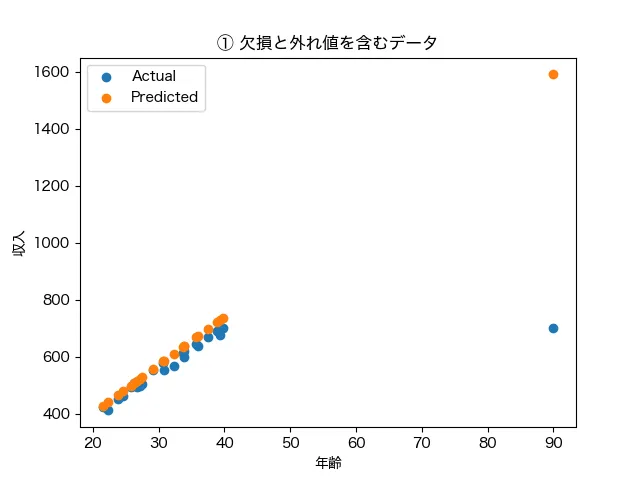
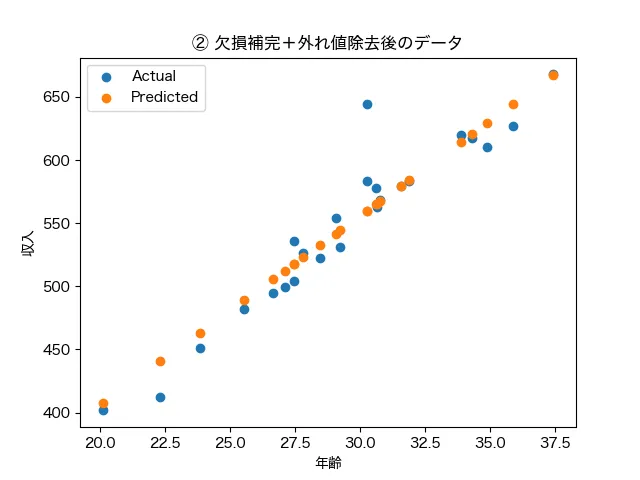
左のデータパターン①では年齢90歳のデータが外れ値として収入の予測値を引き上げています。また、欠損値は予測モデルに反映されないめそのデータも除外された結果、さらに、見当違いの予測に拍車をかけているとう結果です。一方で前処理を行ったデータパターン②では、綺麗に年齢によって収入が予測できています。
このように、欠損値や外れ値は予測への悪影響を与えるため、しっかりと対処しなければダメですね!それでは、実際の欠損値への対処法について3つの方法を見ていきましょう。
欠損値処理法1:欠損値を含む列を削除する
予測モデルを構築する際、データに欠損値が含まれていることはよくあります。この時、もっともシンプルな対処法のひとつが、欠損値を含む列を丸ごと削除する方法です。
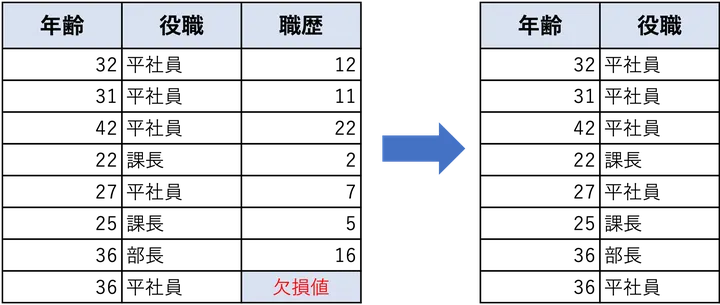
この方法は、実装も考え方も、めちゃめちゃ簡単で、「欠損値がある項目は、ぜんぶ消してしまえ!」という大雑把な考え方です。とはいえ、データに欠損があることでエラーを引き起こすモデルもあるため、この方法はある意味安全面を考えたら、馬鹿にできない方法ともいえます。
例えば、Pythonプログラムに馴染みのある方なら、次の1文で
# pandasで欠損値を含む列を削除する
df_dropped = df.dropna(axis=1)欠損値が含まれているすべての列が削除され、クリーンなデータフレームが得られます。とくに欠損値が多くの列にわずかずつ含まれているような場合、一括で処理したいときには便利です。
とは言っても、この方法には大きな落とし穴もあります。それは、重要な情報を失ってしまう可能性があるという点です。
たとえば、10,000行のデータがあり、ある重要な列にたった1つだけ欠損があるとします。この方法では、その1つの欠損のために、列全体が削除されてしまいます。本来であれば非常に有益な情報を含んでいたかもしれない列を、単純に削除してしまうことで、モデルの予測精度に悪影響を与えることがあります。
そのため、この方法は以下のような限定的なケースでの使用に止めるべきでしょう。
- 欠損率が非常に高く、そもそも列としての信頼性が低い
- 分析や予測において、その列の重要度が低い
- まずは簡易的に前処理を済ませたい段階
欠損値処理は、どのような分析を目的とするか、どの程度の精度を求めるかによって選ぶべき方法が異なります。最も簡単な方法である列の削除は、「とりあえず動くものを作りたい」場面では有効ですが、本番モデルでは注意が必要です。
欠損値処理法2:補完(Imputation)で値を埋める
欠損値処理の中でも、現場でよく使われる実践的な方法が補完(Imputation)です。これは、欠損している値を何らかの値で埋めるという考え方です。
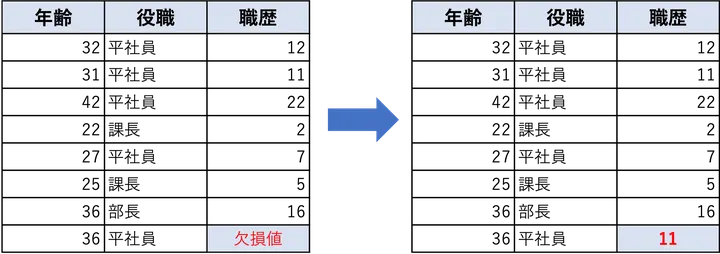
最も基本的な方法としては、列ごとの平均値や中央値や最頻値で欠損を埋めるというやり方があります。たとえば、数値データであれば平均や中央値を使い、カテゴリ変数であれば最も頻繁に出現する値を使うのが一般的です。
この方法の利点は、データを捨てずに活用できる点にあります。前のステップで紹介した「列ごと削除」では、重要な情報が含まれる列であっても削除せざるを得ませんでした。しかし、補完を使えば、その情報を温存しつつ、モデルにデータを渡すことができます。
もちろん、補完によって埋めた値は正確な値ではないため、多少の誤差を生みますが、僕に経験上、多くの場合で何もない状態よりは(やらないよりはマシな程度で)予測精度が向上します。特に、欠損値が少ない場合は、平均や中央値での補完でも十分に有効な手法となります。
ただし、欠損がランダムではなく特定のパターンで発生している場合は、単純な補完では不十分なことがあります。そのようなケースでは、後述する欠損フラグの追加なども検討すべきでしょう。
参考として、pythonのPandasで平均値で補完するコードを以下に示します。
# 平均値で補完する方法(数値型)
df['age'] = df['age'].fillna(df['age'].mean())fillna()はとても便利な機能で、欠損値を自動で識別し、そのデータに平均や中央値や最頻値など指定した方法でデータを補完してくれます。
欠損値処理法3:補完と欠損フラグの併用
欠損値を処理する上で、補完(imputation)は非常に一般的な方法です。しかし、補完だけでは不十分な場合もあります。たとえば、ある値が欠損しているという事実そのものに意味がある場合です。このようなケースでは、補完に加えて「欠損があったこと」を示すフラグを追加することで、モデルがより正確な予測を行えるようになります。
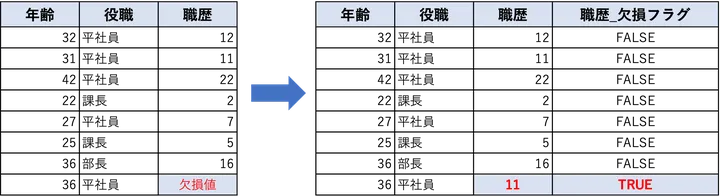
この方法ではまず、通常どおり平均値や中央値などで欠損値を補完します。その上で、元々欠損があった位置に対して「この値は欠損だったかどうか」を示す新たな列(欠損フラグ)を作成します。これにより、モデルは「埋められた値」なのか「元から存在した値」なのかを区別できるようになります。
このアプローチは特に、欠損がランダムでない場合や、特定の属性グループに偏って発生している場合に効果を発揮します。たとえば、ある年齢層の人だけに欠損が集中している場合など、欠損の有無自体が予測に有効な情報になることがあります。
ただし、すべてのケースでこの方法が有効とは限りません。欠損が完全にランダムに発生している場合や、欠損の割合がごくわずかである場合には、欠損フラグを追加しても予測精度が大きく向上することはないかもしれません。そのため、実際にスコアを比較しながら使うかどうかを判断することが重要です。
参考として、平均値補完と欠損フラグを同時に処理するPythonコードを以下に示します。
# 欠損フラグの追加と補完
df['age_missing'] = df['age'].isnull().astype(int) # 欠損があれば1、なければ0
df['age'] = df['age'].fillna(df['age'].mean()) # 平均で補完
欠損値処理による予測精度の改善を比較してみる
では最後に、これまで紹介した欠損値の3つのパターンを、段階をおって実行することで、徐々に予測精度が改善していく様子を見ていきましょう。
今回のシミュレーションではダミーデータを使用します。データの内容は「中古住宅の価格」を予測するモデルを構築し、説明変数として「築年数」「駅からの距離」「広さ」の3つを使用するとします。そのうち、「築年数」と「駅からの距離」に意図的に欠損値を加え、各パターンの欠損値処理がモデルの予測性能にどのような影響を与えるかを検証します。
データの初めの10件は次のとおりです。
| 築年数 | 駅からの距離 | 広さ | 価格 |
|---|---|---|---|
| nan | 15.6495 | 66.3082 | 2034.78 |
| 22.0008 | 5.95672 | 67.6062 | 2699.48 |
| 24.8937 | 6.18855 | 80.9966 | 2485.06 |
| nan | 12.9082 | 76.5526 | 2123.36 |
| nan | 6.48063 | 76.4013 | 2432.78 |
| 15.1136 | 15.8309 | 53.8304 | 2420.96 |
| 24.7504 | 8.75914 | 69.7567 | 2281.9 |
| 19.2432 | 7.75764 | 62.6197 | 2416.95 |
| 19.4839 | nan | 72.7992 | 2485.3 |
| 22.053 | 14.4415 | 69.0185 | 2350.94 |
データ中のnanというのが欠損値に当たります。
それでは、3つの方法で欠損値処理を行い、それぞれのケースについて予測モデルを立てていきましょう。
① 欠損値を含む行をすべて削除
最もシンプルな方法である「欠損行の削除」では、欠損が発生している行をすべて除外します。今回のデータでは「築年数」と「駅からの距離」に欠損値があるため、列ごと削除し、予測モデルを構築しました。
予測モデルの結果:決定係数R2 = 0.578
決定係数は回帰モデルの評価を行う指標で、値が1に近ければ近いほど良い指標になります。2つの特徴量を削除しているので、やっぱりそれほどモデルの精度は高くないですね。
② 欠損値を平均値で補完
次に、欠損している値を「平均値」で埋める方法です。これにより、すべてのデータを使用できるようになり、データの損失を防ぐことができます。
この方法では補完された値は推定値であるため、若干の誤差を含みますが、予測精度としては実用的なレベルで改善することが多いです。こんな感じで、上述のデータは欠損値を埋めています。
| 築年数 | 駅からの距離 | 広さ | 価格 |
|---|---|---|---|
| 18.6427 | 15.6495 | 66.3082 | 2034.78 |
| 22.0008 | 5.95672 | 67.6062 | 2699.48 |
| 24.8937 | 6.18855 | 80.9966 | 2485.06 |
| 18.6427 | 12.9082 | 76.5526 | 2123.36 |
| 18.6427 | 6.48063 | 76.4013 | 2432.78 |
| 15.1136 | 15.8309 | 53.8304 | 2420.96 |
| 24.7504 | 8.75914 | 69.7567 | 2281.9 |
| 19.2432 | 7.75764 | 62.6197 | 2416.95 |
| 19.4839 | 10.0526 | 72.7992 | 2485.3 |
| 22.053 | 14.4415 | 69.0185 | 2350.94 |
モデルの精度は以下のとおりです。①に比べ若干、改善されています。
予測モデルの結果:決定係数R2 = 0.605
③ 平均値で補完+欠損フラグの追加
最後に、②の平均補完に加え、「どのデータが欠損だったのか」を示すフラグを新たな列として追加する方法です。
これは、欠損が完全な偶然ではなく、何らかの傾向に基づいて発生している場合に特に有効です。たとえば、「築年数が古い物件ほど記録が欠損している」といった背景がある場合、モデルがその傾向を学習に活かせる可能性があります。補完後のデータはこんな感じです。
| 築年数 | 駅からの距離 | 広さ | 価格 | 築年数欠損 | 駅距離欠損 |
|---|---|---|---|---|---|
| 18.6427 | 15.6495 | 66.3082 | 2034.78 | 1 | 0 |
| 22.0008 | 5.95672 | 67.6062 | 2699.48 | 0 | 0 |
| 24.8937 | 6.18855 | 80.9966 | 2485.06 | 0 | 0 |
| 18.6427 | 12.9082 | 76.5526 | 2123.36 | 1 | 0 |
| 18.6427 | 6.48063 | 76.4013 | 2432.78 | 1 | 0 |
| 15.1136 | 15.8309 | 53.8304 | 2420.96 | 0 | 0 |
| 24.7504 | 8.75914 | 69.7567 | 2281.9 | 0 | 0 |
| 19.2432 | 7.75764 | 62.6197 | 2416.95 | 0 | 0 |
| 19.4839 | 10.0526 | 72.7992 | 2485.3 | 0 | 1 |
| 22.053 | 14.4415 | 69.0185 | 2350.94 | 0 | 0 |
右端の2列は、対応する列で欠損値のあった行に1を立ててあります。
これによって、回帰モデルは次のような結果でした。
予測モデルの結果:決定係数R2 = 0.723
見事、3つの処理の中で一番、決定係数は高くモデルの精度が向上してることがわかりました!
最後に上記のシミュレーションデータの生成とモデル構築のpythonプログラムを掲載しておきます。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
# ダミーデータ生成
np.random.seed(0)
n = 100
# 特徴量(日本語)
築年数 = np.random.normal(20, 5, n)
駅からの距離 = np.random.normal(10, 3, n)
広さ = np.random.normal(70, 10, n)
# ターゲット(価格)
価格 = 3000 - 25 * 築年数 - 20 * 駅からの距離 + 3 * 広さ + np.random.normal(0, 100, n)
df = pd.DataFrame({
'築年数': 築年数,
'駅からの距離': 駅からの距離,
'広さ': 広さ,
'価格': 価格
})
# 築年数に非ランダム欠損、駅からの距離にランダム欠損
df_missing = df.copy()
df_missing.loc[df_missing['築年数'] > 25, '築年数'] = np.nan
df_missing.loc[np.random.choice(df.index, 10, replace=False), '駅からの距離'] = np.nan
# 評価関数(グラフ付き)
def evaluate(df_input, desc, use_flags=False):
df_clean = df_input.copy()
if not use_flags:
df_clean = df_clean.dropna()
X = df_clean[['築年数', '駅からの距離', '広さ']]
else:
X = df_clean[['築年数', '駅からの距離', '広さ', '築年数欠損', '駅距離欠損']]
y = df_clean['価格']
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
model = LinearRegression()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
r2 = r2_score(y_test, y_pred)
print(f"{desc} → 決定係数 R²: {r2:.3f}")
# ① 欠損行の削除
df_drop_rows = df_missing.dropna()
evaluate(df_drop_rows, "① 欠損行を削除")
# ② 平均値で補完
df_mean_impute = df_missing.copy()
df_mean_impute['築年数'] = df_mean_impute['築年数'].fillna(df_mean_impute['築年数'].mean())
df_mean_impute['駅からの距離'] = df_mean_impute['駅からの距離'].fillna(df_mean_impute['駅からの距離'].mean())
evaluate(df_mean_impute, "② 平均値で補完")
# ③ 平均値補完+欠損フラグ追加
df_flag_impute = df_missing.copy()
df_flag_impute['築年数欠損'] = df_flag_impute['築年数'].isnull().astype(int)
df_flag_impute['駅距離欠損'] = df_flag_impute['駅からの距離'].isnull().astype(int)
df_flag_impute['築年数'] = df_flag_impute['築年数'].fillna(df_flag_impute['築年数'].mean())
df_flag_impute['駅からの距離'] = df_flag_impute['駅からの距離'].fillna(df_flag_impute['駅からの距離'].mean())
evaluate(df_flag_impute, "③ 補完+欠損フラグ", use_flags=True)
外れ値の処理について
これまで、欠損値の処理について詳しくまとめましたが、外れ値については欠損値ほど決まった対処法があるわけではなく、そのデータを見ながら状況に合わせて対処するということが多いです。というのも、「欠損値はデータがなければ明らかに欠損値と定義できる」のですが、外れ値は「データ分析者が外れ値と定義しなければいけない」という性質上、欠損値ほど機械的に対処が難しいためです。
とはいえ、何も対処しないわけにはいかないので、僕自身は実務では大まかに以下のような対処をしています。
外れ値の主な処理方法
1. 削除する
- 外れ値が明らかに入力ミスや計測エラーと考えられる場合は、行ごと削除するのがシンプルです。
- 例:年齢が「-5」や「200」など、明らかに不自然な値。
- スピーディーに結果を出さないといけない実務上では、結構、これで乗り切ることが多い。
2. クリッピング(上限・下限を設定)する
- 値の範囲を制限し、外れ値をある上限や下限でカットする方法。
- 例:年収が1億円を超えた人を「1億円」と扱うなど。
- 上限を決める時にその上限に意味がある場合はこれでいいが、そうでないと、実務上では決定しずらい。
3. 変換する(ロジスケール・対数変換など)
- 外れ値の影響を緩和するために、スケールを変える方法。
- 対数変換(
np.log())やBox-Cox変換などが代表例です。 - とはいえ、変換しても外れ値が残ることは往々にしてある。
4. カテゴリ分割する
- 外れ値を「特異カテゴリ」として扱い、カテゴリ変数として処理する方法。
- 例:「通常」「高値」「異常値」などに分けてワンホットエンコーディングする。
- 予測モデルを構築するのであれば、やった方がいい。
5. 外れ値に強いモデルを使う
- ランダムフォレストやブースティング系のモデルは、外れ値に比較的強いため、あえて特別な処理をしないという選択肢。
外れ値対処法の整理
これらの方法の中からどれを選ぶかは、目的やデータの性質によって判断する必要があります。たとえば、単純な集計や可視化をするだけであれば、あえて外れ値を残して「どんなデータが異常なのか」を見極めるほうが有益なこともあります。
一方で、機械学習モデルの精度を重視したい場合には、外れ値が学習を大きく歪めることがあるため、何らかの対応をすることが望ましいです。
また、外れ値を完全に除去するのではなく、「どのデータが外れ値だったか」をフラグ化して特徴量として使うという手法もあります。これは、欠損値処理で補完+欠損フラグを追加するのと同じ発想で、外れ値の存在自体をモデルに学ばせるアプローチです。
最後に大切なのは、「外れ値=悪」ではなく、外れ値は時に重要なシグナルであるという意識を持つことです。
実務でも、「これは明らかにミスだな」と思う外れ値と、「もしかしたら実際にあったことかもしれない」という外れ値は区別して扱うようにしています。
結局のところ、外れ値に対して機械的な正解は存在しないからこそ、データの背景や目的に応じた柔軟な判断が求められるのだと思います。
まとめ
以上、本記事では、予測精度を高めるための欠損値と外れ値の対処法について解説しました!欠損値には、行削除・平均補完・補完+フラグ追加といった基本的な3つの手法があり、状況に応じて使い分けることが重要です。一方、外れ値は「何が外れ値か」を定義する必要があるため、削除・クリッピング・変換・カテゴリ化・外れ値に強いモデルの活用など柔軟な対応が求められます。どちらもデータの背景を理解し、目的に合わせて最適な前処理を選ぶことが、精度の高いモデル構築への第一歩です。
これらを使うことで、予測精度の向上も見込めます。ぜひ、実務でもコンペでも活用してみてください!
