こんにちは、デジタルボーイです。今回は予測モデルの選定手順について、ホールドアウトとクロスバリデーションを踏まえつつ、Pythonプログラミングを使いながら解説したいと思います。

デジタルボーイです。
データサイエンス歴20年以上のおっさんです。中小企業診断士として、データサイエンス、WEBマーケティング、SEOに関するデータ分析、コンサルティングの仕事をしています。自己紹介の詳細はコチラ
はじめに
僕自身、機械学習で予測モデルを作るとき、どのモデルを最終的に採用すべきか、迷うことはよくあります。線形回帰、ランダムフォレスト、XGBoost…どれが一番良いかは、データや目的によって変わってきます。そのため、「モデル選定」というステップがとても重要になります。
この記事では、予測モデルの選び方について、ホールドアウト法や交差検証(CV)といった評価方法を使いながら、どのようにして最適なモデルを決めていくかを実例とともに紹介します。
「なんとなく有名だからこのモデルでいいや」ではなく、ちゃんと根拠を持ってモデルを選べるようになると、分析の質がぐっと上がりますよ!初心者の方にもわかりやすく説明していくので、安心して読み進めてくださいね。
予測モデル選定に必要な基礎知識
予測モデルを選ぶうえで大切なのは、「そのモデルがどれだけ良い性能を発揮しているのか」を正しく評価することです。ここでは、その評価方法としてよく使われるホールドアウト法と交差検証(Cross Validation)について、初心者の方にもわかりやすく解説します。
ホールドアウト法とは?
ホールドアウト法は、データを「学習用」と「テスト用」に分けて使う評価方法です。たとえば、全体のデータの80%を学習用、残りの20%をテスト用にして、モデルの性能をテスト用データで確認します。

この方法はシンプルで実装も簡単なので、まず試してみるにはぴったりです。ただし、評価結果が使ったテストデータに大きく左右されるため、データの分け方によって精度が大きくブレることもあります。
クロスバリデーション(CV:交差検証)とは?
クロスバリデーションで、特に代表的手法である「K分割交差検証(K-Fold CV)」は、データをK個に分けて、K回モデルを学習・評価する方法です。たとえばK=5なら、データを5分割して、毎回1つをテスト用、残り4つを学習用にする…というのを5回繰り返します。

これにより、データ全体をバランスよく評価に使うことができ、精度のブレが少なく安定した評価が得られるというメリットがあります。
ただし、ホールドアウトに比べて計算コストが高い(時間がかかる)という点には注意が必要です。
どっちがいい?
どちらの方法も「本当にそのモデルが良いのか?」を確かめるためには欠かせない技術です。特に実務やコンペでは、交差検証がほぼ標準の評価手法になっています。モデルをただ作るだけでなく、しっかり評価して選ぶという意識を持つことが大切ですね!
モデル選定のための指標
予測モデルを評価するときに欠かせないのが「指標(スコア)」です。どんなに手間をかけてモデルを作っても、何をもって「良い」とするかの基準がなければ比較も選定もできません。
ここでは、回帰タスクと分類タスクに分けて、よく使われる指標を紹介しながら、目的に応じてどう選ぶべきかについても解説します。
回帰タスクの指標
回帰タスクとは、売上や価格、体重などの「連続する数値」を予測する問題です。代表的な評価指標は以下の通りです。
MSE(平均二乗誤差)
誤差を2乗して平均したもので、大きな誤差ほどペナルティが大きくなります。外れ値に敏感です。
MAE(平均絶対誤差)
誤差の絶対値を平均したもので、外れ値の影響を受けにくく、直感的にもわかりやすいです。
R²(決定係数)
予測がどれだけ正確に元のデータを説明できているかの割合です。1に近いほどモデルの説明力が高いとされます。
R²は一見わかりやすく感じますが、過学習モデルでも高くなることがあるため、MSEやMAEと併用して判断するのが望ましいです。
分類タスクの指標
分類タスクでは、スパム判定や病気の有無など、カテゴリに分ける予測を行います。ここでもいろいろな指標があります。
Accuracy(正解率)
全体のうち、正しく予測できた割合。わかりやすいですが、クラスのバランスが悪い場合は過信できません。
Precision(適合率)
予測したうち、どれだけ正しく「当たり」を出せたか。たとえば不正検出で「不正」と予測したものの中に、どれだけ本当に不正があったかを示します。
Recall(再現率)
実際の「当たり」のうち、どれだけ見逃さずに予測できたか。病気の検出など、見逃しが致命的な場面で重要です。
F1-score
PrecisionとRecallのバランスを取った指標です。どちらも大事なときに使います。
分類の指標については以下にも詳しく解説してあるので、よかったら参考にしてください。

目的に応じた指標の選び方
指標を選ぶときに大切なのは、何を重視したいか」を明確にすることです。
たとえば:
- 商品価格の予測なら誤差の大きさを重視するので MAE や MSE
- 病気の発見なら見逃しが怖いので Recall
- スパムメールの判定なら誤検知を減らしたいので Precision
- 全体的な性能評価をしたいときは AUC や F1-score
このように、指標の選定は、目的と現場のリスク感覚に基づいて慎重に決める必要があります。数字だけを見るのではなく、「その数字が現場で何を意味するか」を考えることが、よいモデル選びへの第一歩です!
実験:ホールドアウト vs クロスバリデーションでモデル選定してみた!
最後に、実際に複数の回帰モデルを使って、ホールドアウト法とクロスバリデーション(CV)それぞれでモデル性能を比較します。可視化には「予測値 vs 実測値の散布図」、指標には「決定係数(R²)」を用いて、モデル選定の流れを追っていきます。
使用データとモデル一覧
- データセット:California Housing(scikit-learn内のオープンデータ)
- 予測対象:住宅価格(正確には「中央値」)
- 使用モデル:
- Linear Regression(線形回帰)
- SVR(RBFカーネル)
- Decision Tree
- Random Forest
- Gradient Boosting Regressor
実験1:ホールドアウト法による評価
まずはデータを 訓練データ80%、テストデータ20% に分割し、各モデルを学習・予測してテストR²を比較しました。予測モデルの性能結果は以下のとおりです。
| モデル | 学習データR² | テストデータR² |
|---|---|---|
| 線形回帰モデル | 0.613 | 0.576 |
| SVR (RBFカーネル) | 0.749 | 0.728 |
| 決定木 | 1.000 | 0.622 |
| ランダムフォレスト | 0.974 | 0.805 |
| Gradient Boosting | 0.805 | 0.776 |
決定係数R2は、1に近いほどモデルがデータにフォットしている判断できる指標です。決定木は学習データでは1であり完全にデータにモデルがフィットしていますが、テストデータでは0.622と悪化しており、典型的な過学習であることがわかります。
散布図(ホールドアウト)
以下の散布図は、実測値と予測値の比較を表しています。黒い破線は理想的な「実測=予測」のラインです。また青色が学習用データ、赤色がテスト用のデータのプロットです。
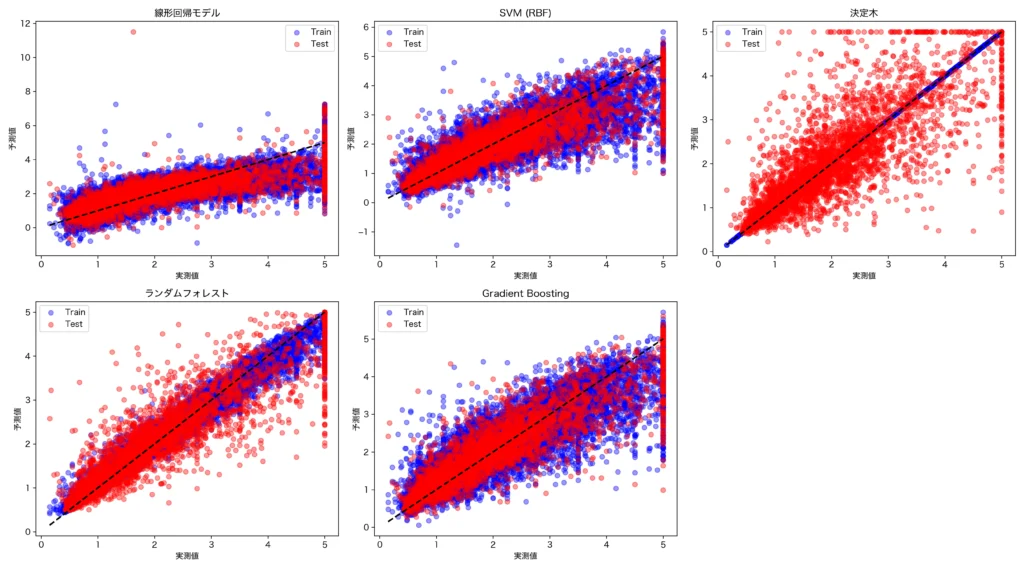
例えば右上の決定木のプロットでは、青色のプロットである学習データではほとんどが右上がりの点線乗にあるにもかかわらず、予測値である赤色の点はばらついており、過学習の様子がプロットからも見て取れます。
ホールドアウトによるモデル選定
以上の結果から、ランダムフォレストのR2乗値は学習データで0.974、テストデータで0.805であり、学習データとテストデータの両者でモデルのフィットが高く、他のモデルを凌いでいることがわかります。これよりこのケースでは予測モデルには、ランダムフォレストを選定すべきと考えます。
Pythonコード
以下はホールドアウトの実験で使ったコードです。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.svm import SVR
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from sklearn.metrics import r2_score
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
plt.rcParams['font.family'] = 'Hiragino sans'
# データ読み込み
data = fetch_california_housing()
X, y = data.data, data.target
# 訓練データ・テストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# モデル一覧(必要なものはStandardScalerで前処理)
models = {
'線形回帰モデル': Pipeline([
('scaler', StandardScaler()),
('model', LinearRegression())
]),
'SVM (RBF)': Pipeline([
('scaler', StandardScaler()),
('model', SVR(kernel='rbf'))
]),
'決定木': DecisionTreeRegressor(random_state=42),
'ランダムフォレスト': RandomForestRegressor(random_state=42),
'Gradient Boosting': GradientBoostingRegressor(random_state=42)
}
# プロット準備
plt.figure(figsize=(18, 10))
# 各モデルで処理
for i, (name, model) in enumerate(models.items(), 1):
model.fit(X_train, y_train)
# 予測
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)
# R²スコア
r2_train = r2_score(y_train, y_train_pred)
r2_test = r2_score(y_test, y_test_pred)
print(f"🔍 {name}")
print(f" 訓練データ R²: {r2_train:.3f}")
print(f" テストデータ R²: {r2_test:.3f}\n")
# 散布図
plt.subplot(2, 3, i)
plt.scatter(y_train, y_train_pred, color='blue', alpha=0.4, label='Train')
plt.scatter(y_test, y_test_pred, color='red', alpha=0.4, label='Test')
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=2)
plt.title(name)
plt.xlabel("実測値")
plt.ylabel("予測値")
plt.legend()
plt.tight_layout()
plt.savefig("california_housing_regression.webp",format="webp",dpi=300)
plt.show()
実験2:クロスバリデーションによる評価
今回はk=5でデータを分割しクロスバリデーションを実施しました。予測モデルの性能結果は以下のとおりです。
| モデル | 5回の平均R² |
|---|---|
| 線形回帰モデル | 0.601 |
| SVR (RBFカーネル) | 0.742 |
| 決定木 | 0.616 |
| ランダムフォレスト | 0.81 |
| Gradient Boosting | 0.788 |
5等分したデータの5回の平均R²を算出しています。結果はランダムフォレストが最も高いことはホールドアウトと変わりません。ただし、ホールドアウトはモデルの訓練に20%を無駄にしているため、この点で将来の予測精度はクロスバリデーションの方が高いことが期待されます。
また、実測値と予測値の散布図は以下となります。今回では特にモデルのフィットの悪かった線形回帰モデルと決定木では、黒い点線から、点がばらついている様子が見て取れます。
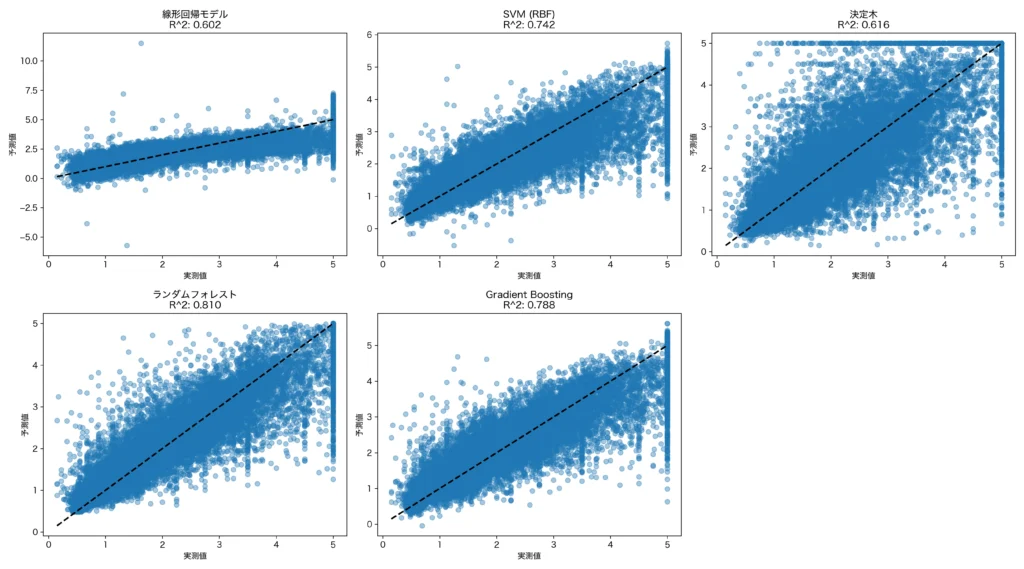
クロスバリデーションによるモデル選定
以上の結果から、ランダムフォレストのR2乗値は0.81であり、最もデータにフィットしたモデルという結果でした。これよりこのケースでは予測モデルには、ランダムフォレストを選定すべきと考えます。
Pythonコード
以下はクロスバリデーション実験で使用したコードです。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import cross_val_score, cross_val_predict, KFold
from sklearn.linear_model import LinearRegression
from sklearn.svm import SVR
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import r2_score
# データ取得
data = fetch_california_housing()
X, y = data.data, data.target
# モデルの定義(スケーリングが必要なものはPipelineに)
models = {
'線形回帰モデル': Pipeline([
('scaler', StandardScaler()),
('model', LinearRegression())
]),
'SVM (RBF)': Pipeline([
('scaler', StandardScaler()),
('model', SVR(kernel='rbf'))
]),
'決定木': DecisionTreeRegressor(random_state=42),
'ランダムフォレスト': RandomForestRegressor(random_state=42),
'Gradient Boosting': GradientBoostingRegressor(random_state=42)
}
# クロスバリデーション設定
cv = KFold(n_splits=5, shuffle=True, random_state=42)
# プロット準備
plt.figure(figsize=(18, 10))
# モデルごとに評価&可視化
for i, (name, model) in enumerate(models.items(), 1):
# CVスコア(R^2)
scores = cross_val_score(model, X, y, cv=cv, scoring='r2')
print(f"🔍 {name}")
print(f" R^2 平均: {scores.mean():.3f}, 標準偏差: {scores.std():.3f}")
# CV予測
y_pred = cross_val_predict(model, X, y, cv=cv)
# 全体R^2
overall_r2 = r2_score(y, y_pred)
print(f" cross_val_predict による全体R^2: {overall_r2:.3f}\n")
# 散布図プロット
plt.subplot(2, 3, i)
plt.scatter(y, y_pred, alpha=0.4, label='CV Predictions')
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=2)
plt.title(f"{name}\nR^2: {overall_r2:.3f}")
plt.xlabel("実測値")
plt.ylabel("予測値")
plt.tight_layout()
plt.suptitle("クロスバリデーションによるモデル選定", fontsize=16, y=1.02)
plt.savefig("california_housing_regression_cv.webp",format="webp",dpi=300)
plt.show()
まとめ
以上、予測モデル選定の手順について、とくにホールドアウトとクロスバリデーションの手順に沿って実行しました。ここで紹介した内容はどれも僕自身が実務で使っている手法で、予測モデルの選定に大切なテクニックになります。ぜひ、参考にしてください!
