リッジ回帰とラッソ回帰を徹底解説

こんにちは、デジタルボーイです。今回は回帰モデルの中のモデルである、、リッジ回帰モデルとラッソ回帰モデルについて、メカニズムの解説と、Pythonとscikit-learnによる実装について紹介したいと思います！

リッジ回帰とラッソ回帰は、線形回帰の一種であり、特に多重共線性（特徴量同士が相関しすぎている状態）が問題になる場合に有効な手法です。僕自身、実務場面でもこれらのモデルはかなりの使用頻度があり、おすすめのモデルでもあります。データサイエンティストにとって重要なモデルあることは間違い無いと思いますので、ぜひ、マスターしてみて下さい！

ちなみにこれまで、単回帰分析、重回帰分析についても解説しています。リッジ回帰モデルとラッソ回帰モデルはこれらのモデルの応用モデルと言えるので、必要があれば以下の解説を先におさらいしてみてください。

あわせて読みたい

pythonによる回帰分析、初歩の初歩〜単回帰モデル こんにちは、デジタルボーイです。今回は機械学習や統計モデルの初めの一歩とも言える、単回帰分析について、Pythonとscikit-learnを使い、初歩の初歩について解説した…

あわせて読みたい

pythonによる回帰分析〜重回帰モデル入門 こんにちは、デジタルボーイです。前回は機械学習や統計モデルの初めの一歩とも言える、単回帰分析について学習しました。 データ分析を始めたばかりの方にとって、複数…

記事を書いた人

デジタルボーイです。
データサイエンス歴20年以上のおっさんです。中小企業診断士として、データサイエンス、WEBマーケティング、SEOに関するデータ分析、コンサルティングの仕事をしています。自己紹介の詳細はコチラ

リッジ回帰とラッソ回帰とは？

リッジ回帰とラッソ回帰を説明する前に、簡単に重回帰モデルの説明から入りますね。

重回帰モデルのモデル式と損失関数

簡単のために、説明変数が２つに絞った場合の重回帰モデルを想定してみます。モデル式は次のように表すことができます。

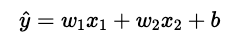
説明変数は２つなので推定する重みもw1とw2の2つで、加えて切片bもモデルで推定します。
また、i番目のデータの予測値は以下のように表すことができます。

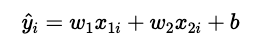
上記の予測式を求めるためには、重みwと切片bを推定する必要があります。そこで必要な考え方として「損失関数」という関数の考え方が重要になってきます。ここでは、最も基本的な損失関数は、二乗誤差（Mean Squared Error: MSE）を例に説明していきます。

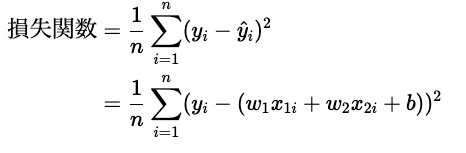
この損失関数を最小化するようなwとbを求めることが、回帰モデルのゴールと言えます。

この損失関数の感覚的な説明は、「目的変数と予測値の差を最小にするように、重みと切片を推定する」ということになります。もう少し厳密にいうと「目的変数と予測値の差の二乗を最小にするように、重みと切片を推定する」ということになります。なぜ、２乗するのかというと、差にはマイナスの差もプラスの差もあるため、そのまま足しあげるとそれらが相殺されてしい、部分的には誤差が大きいのに、全体で見ると誤差が小さくなるということを、避けるためです。

リッジ回帰とラッソ回帰のモデル式と損失関数

実はリッジ回帰もラッソ回帰もモデル式は、重回帰モデルのモデル式と同じです（２変数の場合）。

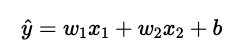
じゃあ、何が違うのかというと、損失関数が違うんですね。

まず、リッジ回帰の損失関数は以下のように表すことができます。

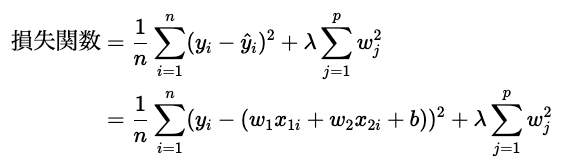
つづいて、ラッソ回帰の損失関数は以下のように表すことができます。

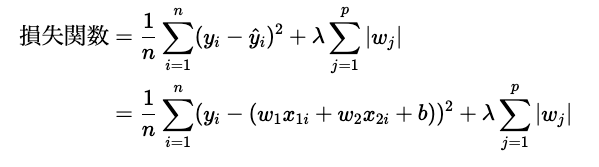
上記のように、損失関数の第１項は、重回帰モデルの回帰モデルと同じです。違うのは第２項になります。この第２項はそれぞれ、正則化項と呼ばれています。正則化項は、モデルが過学習することを防ぐために導入される項で、重みの大きさに対してペナルティを与える効果があります。リッジ回帰では重みwの二乗に、ラッソ回帰では重みwの絶対値にペナルティを与えることで、重みが大きくなりすぎることを抑制します。

正則化項の効果への直感的な理解

先の説明の通り、回帰モデルでは損失関数をできるだけ小さくするように重みを求めていきます。その際、正則化項には重みwが入っているため、重みが大きくなりすぎることを抑制します。

極端な話、同じように損失関数の第１項を同程度に小さくする重みのパターン1のwとパターン２のwがあり、仮にパターン1のw<パターン2のwだった場合、損失関数の第２項（正則化項）はパターン1のwのほうが小さくなります。そのため、損失関数全体では、パターン1のwのほうが小さくなり、パターン1のwの重みが選択されることになります。

じゃあ、なぜ、リッジ回帰とラッソ回帰で２つの正則化項があるのか？という点が次に疑問に上がると思います。

ちなみに、正則化項の効果は、リッジ回帰とラッソ回帰でそれぞれ働く効果が若干違います。

• リッジ回帰は、大きすぎる重みに対して小さくする効果が働きやすい
• ラッソ回帰は、小さな重みに対して0に近づける効果が働きやすい

なぜそうなるのかについて、ここも直感的な理解をえるためにさくっと説明してみます。

説明のために、損失関数は下に凸の関数であり、反復計算で最小化することを考えます（実際には、ラッソ回帰は反復計算で解を求めますが、回帰モデルやリッジ回帰は反復計算をしなくともは求まります。これを解析的に解が求まると言います）。

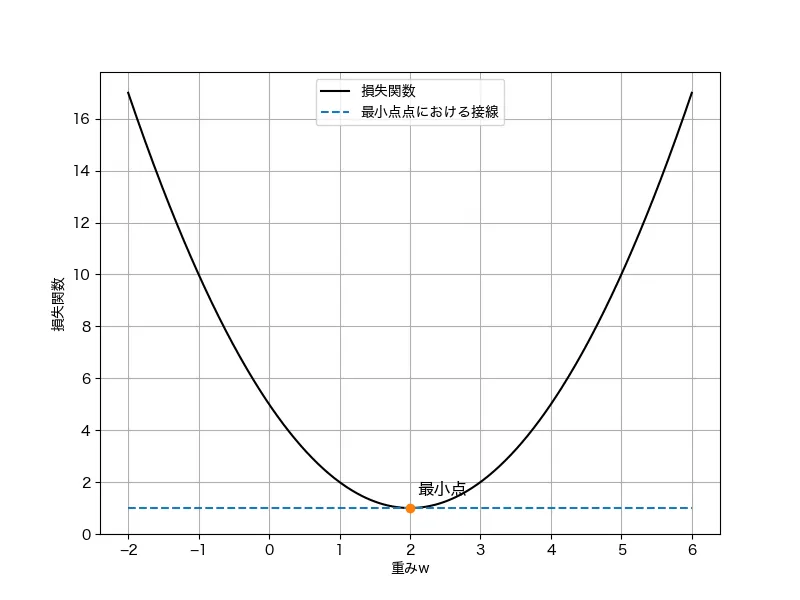
損失関数の最小化の手順は、「損失関数を重みで偏微分した導関数(勾配)が0の時の重みを求める」というものです。これはグラフから理解するとわかりやすいでしょう。損失関数の最小値はグラフの一番下の点です。この最小値の点の特徴は、点の接線は横ばい（勾配が０）であることがわかります。なので、勾配が０の地点の重みが損失関数を最小にする重みである、というように考えるメカニズムになります。

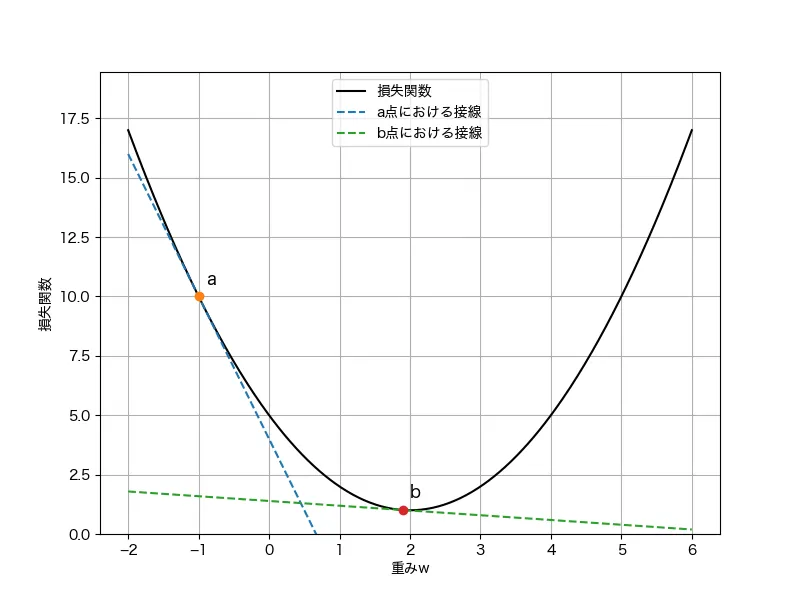
最小化計算では、この損失関数に対して、勾配という方位磁石（コンパス）に従い、探索することで、最小点を見つけるという作業になります。また、一回の計算で探索する（進む）幅は勾配が大きいほど大きいです。これは、グラフでも最小値に遠い方が勾配(点a)が大きく、最小点に近い方（点b）が勾配が小さいことから、直感的に理解できると思います。

同様に、最小化のステップで点aの時点では勾配が大きく（急）、最小値からも遠いので、次の計算時には探索の幅が大きくなります（遠くまで進んでみる）。一方で、点bの時点では勾配が小さく（緩やか）、最小値から近いので、次の探索の幅は小さくなります（ちょっとだけ進んでみる）。

以上の最小化のステップを念頭に、リッジ回帰とラッソ回帰の正則化項の効果を考えてみます。

リッジ回帰の正則化項部分の勾配は計算すると次のようになります。

リッジ回帰の正則化項の勾配

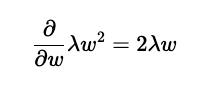
ここから、探索の幅は2λwに比例すると言えます。

ラッソ回帰の正則化項の勾配

一方、ラッソ回帰の正則化項部分の勾配は

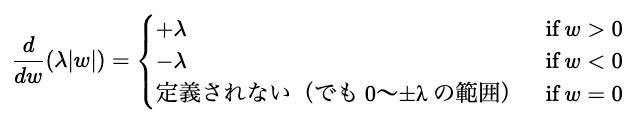
となります。絶対値の微分なので、ちょっとめんどくさいですが、微分後の勾配は±λと思っていただければOKです。探索の幅はλに比例すると言えます。

両者の違いを見ていきましょう。勾配にwが入っているリッジ回帰では、wが大きいほど、次の重みの探索の幅が大きくなります。一方、ラッソ回帰では、勾配にwが入っていないため、探索の幅はwの大きさによらず一律にλ分更新されます。その結果、wの値が小さいほど、更新の煽りを受け0に収束します。

ここからわかることは、リッジ回帰では重みが大きいほど、更新の幅が大きくなるが、ラッソ回帰では重みの大きさによらず、更新の幅が一律にλになるため、小さな重みがゼロに収束しやすいということですね！

その結果、重みはどのように変更されるのかを示したのが次のグラフです。

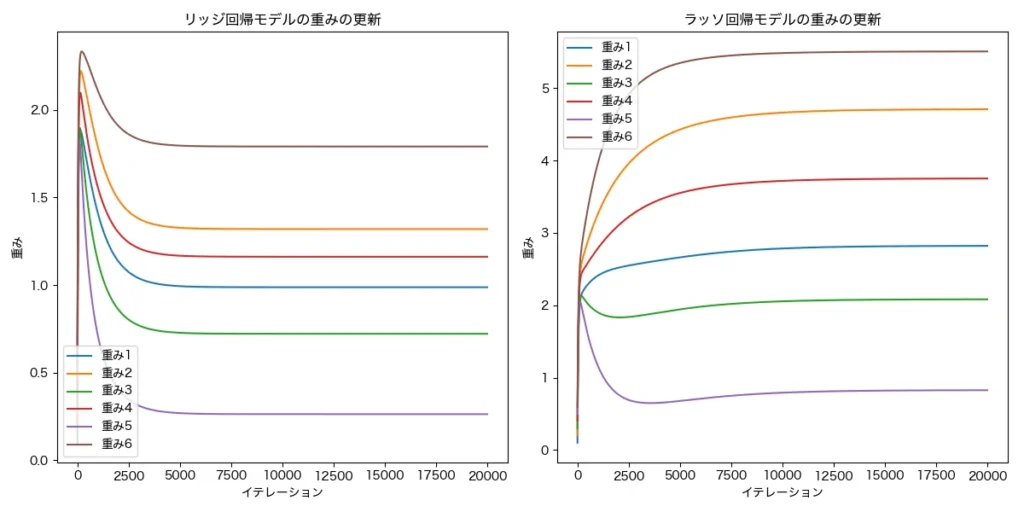
上のグラフでは、リッジ回帰では、最小化のステップで初期段階である程度大きな重みなので、それに対して、ペナルティを与えられている（反復の前半でペナルティが与えられている）ことが見て取れます。

一方、ラッソ回帰では重みの小さい順にペナルティが与えられている様子が見て取れます。ここから、全体的に重みを小さくしたい場合はリッジ回帰、特に重みの小さいものを無視したいときにはラッソ回帰が良さそうですね！

それでは以降ではpythonを使って実装を見ていきましょう

必要なライブラリのインストール

以下のコマンドで必要なライブラリをインストールできます。

pip install scikit-learn matplotlib pandas numpy

pipを使ったインストール方法はこちらになります。

あわせて読みたい

pipでpandasをインストールする方法 こんにちは、デジタルボーイです。備忘録がてら、macとLinuxにpipでpandasをインストールするための手順を、まとめておきます。 記事を書いた人 デジタルボーイです。デ…

あわせて読みたい

pipでnumpyをインストールする方法 こんにちは、デジタルボーイです。備忘録がてら、macとLinuxにpipでNumPyをインストールするための手順を、まとめておきます。 記事を書いた人 デジタルボーイです。デ…

あわせて読みたい

pipでscikit-learn(sklearn)をインストールする方法： こんにちは、デジタルボーイです。備忘録がてら、macとLinuxにpipでscikit-learn(sklearn)をインストールするための手順を、まとめておきます。 記事を書いた人 デジタ…

まずは、必要なライブラリをインポートしましょう。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.metrics import mean_squared_error
from sklearn.datasets import load_diabetes

データの概要（糖尿病データセット）

サンプルデータとして、sklearn.datasets に含まれている 糖尿病データセット（diabetes dataset） を使用します。
このデータセットは、10個の特徴量（年齢、BMI、血圧など）を使って糖尿病の進行度を予測するためのデータです。
load_diabetes() を用いてデータを読み込み、概要を確認しましょう。

# データの読み込み
data = load_diabetes()

# データの特徴量とターゲット変数
X = data.data
y = data.target

# データフレーム化
df = pd.DataFrame(X, columns=data.feature_names)
df["target"] = y

# 先頭5行を表示
print(df.head())

アウトプットはこんな感じです。

このデータセットには 10個の特徴量 があり、それぞれが糖尿病の進行度に関連しています。また、target 列が予測対象（目的変数）になります。

それぞれのデータの意味は以下となります。

特徴量の説明

分析の目的とゴール

モデル実装

以下のコードでモデルを構築します。

# 必要なライブラリをインポート
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.metrics import mean_squared_error, r2_score
import numpy as np

# データの準備
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 特徴量の標準化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# 重回帰モデル
lr = LinearRegression()
lr.fit(X_train_scaled, y_train)
y_pred_lr = lr.predict(X_test_scaled)

# リッジ回帰モデル（α=1.0）
ridge = Ridge(alpha=1.0)
ridge.fit(X_train_scaled, y_train)
y_pred_ridge = ridge.predict(X_test_scaled)

# Lasso回帰モデル（α=1.0）
lasso = Lasso(alpha=1.0)
lasso.fit(X_train_scaled, y_train)
y_pred_lasso = lasso.predict(X_test_scaled)

モデル評価

では、構築したモデルを評価してみましょう。

# 重回帰モデルの評価指標
mse_lr = mean_squared_error(y_test, y_pred_lr)
rmse_lr = np.sqrt(mse_lr)
r2_lr = r2_score(y_test, y_pred_lr)

print("重回帰モデル:")
print(f"MSE: {mse_lr:.2f}")
print(f"RMSE: {rmse_lr:.2f}") 
print(f"R²: {r2_lr:.2f}")
print()

# リッジ回帰モデルの評価指標
mse_ridge = mean_squared_error(y_test, y_pred_ridge)
rmse_ridge = np.sqrt(mse_ridge)
r2_ridge = r2_score(y_test, y_pred_ridge)

print("リッジ回帰モデル:")
print(f"MSE: {mse_ridge:.2f}")
print(f"RMSE: {rmse_ridge:.2f}")
print(f"R²: {r2_ridge:.2f}")
print()

# Lasso回帰モデルの評価指標
mse_lasso = mean_squared_error(y_test, y_pred_lasso)
rmse_lasso = np.sqrt(mse_lasso)
r2_lasso = r2_score(y_test, y_pred_lasso)

print("Lasso回帰モデル:")
print(f"MSE: {mse_lasso:.2f}")
print(f"RMSE: {rmse_lasso:.2f}")
print(f"R²: {r2_lasso:.2f}")

アウトプットはこんな感じでした。

重回帰モデル:
MSE: 2900.19
RMSE: 53.85
R²: 0.45

リッジ回帰モデル:
MSE: 2892.01
RMSE: 53.78
R²: 0.45

Lasso回帰モデル:
MSE: 2824.57
RMSE: 53.15
R²: 0.47

モデルの評価の解説

3つの回帰モデルで予測精度を比較した結果、ラッソ回帰モデルが最も良い性能を示しました。

• 重回帰モデルは基本形で、R²は0.45、予測誤差（RMSE）は53.85。そこそこの精度ですが、やや過学習のリスクもあります。
• リッジ回帰モデルは重回帰とほぼ同じ結果で、正則化（L2）によって多少の安定性が加わる程度でした。
• ラッソ回帰モデルはMSEが最も低く、R²も0.47と最も高く、最も良好な予測性能を発揮しました。L1正則化によって不要な特徴量を自動で抑える効果が、モデルの改善に寄与したと考えられます。

今回のモデルの決定係数は0.45~0.47でした。現実場面ではこの数値だと、「使い物にならないくらい精度の低い」モデルですかね（汗）。今回はモデルの紹介が目的なので、こんなもんにしときましょう（焦）

アウトプットのグラフ化

予測結果を 実際の値（正解データ）と比較 し、どの程度正確に予測できているかを可視化します。さらに、 相関係数（ピアソンの相関） を計算し、予測値と実測値の関連性を数値で示しましょう。

import matplotlib.pyplot as plt
import numpy as np

# フォント設定（Macの場合）
plt.rcParams["font.family"] = "Hiragino sans"

# 3つのサブプロットを作成
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(15, 5))

# 重回帰モデルの散布図
correlation_lr = np.corrcoef(y_test, y_pred_lr)[0, 1]
ax1.scatter(y_test, y_pred_lr, alpha=0.7, edgecolors="k")
ax1.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], "r--")
ax1.set_xlabel("実測値（y_test）")
ax1.set_ylabel("予測値（y_pred）")
ax1.set_title(f"重回帰モデル\n（相関係数: {correlation_lr:.2f}）")
ax1.grid(True)

# リッジ回帰モデルの散布図
correlation_ridge = np.corrcoef(y_test, y_pred_ridge)[0, 1]
ax2.scatter(y_test, y_pred_ridge, alpha=0.7, edgecolors="k")
ax2.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], "r--")
ax2.set_xlabel("実測値（y_test）")
ax2.set_ylabel("予測値（y_pred）")
ax2.set_title(f"リッジ回帰モデル\n（相関係数: {correlation_ridge:.2f}）")
ax2.grid(True)

# Lasso回帰モデルの散布図
correlation_lasso = np.corrcoef(y_test, y_pred_lasso)[0, 1]
ax3.scatter(y_test, y_pred_lasso, alpha=0.7, edgecolors="k")
ax3.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], "r--")
ax3.set_xlabel("実測値（y_test）")
ax3.set_ylabel("予測値（y_pred）")
ax3.set_title(f"Lasso回帰モデル\n（相関係数: {correlation_lasso:.2f}）")
ax3.grid(True)

plt.tight_layout()
plt.show()

結果はこんな感じでした。

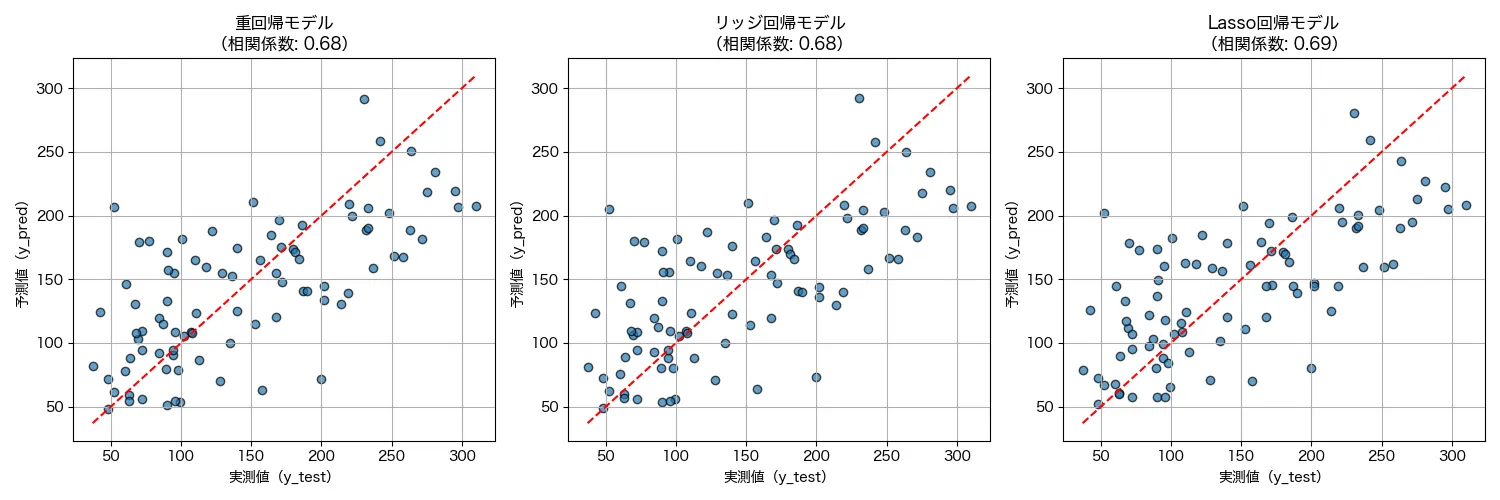
相関係数が０.６８~0.69ということで、概ね、右肩上がりの関係性で、「実測値が上がれば予測値も直線的に上がっている」がとなっていますね！

モデルの回帰係数の確認

リッジ回帰とラッソ回帰では、通常の線形回帰と異なり、係数（重み）が 正則化によって抑制 されます。ここでは、モデルが学習した 回帰係数（weight, β） を可視化し、各特徴量の影響度を確認します。

# 各モデルの回帰係数を取得
lr_coefficients = lr.coef_
ridge_coefficients = ridge.coef_
lasso_coefficients = lasso.coef_

# 特徴量名と回帰係数をデータフレーム化
lr_df = pd.DataFrame({"特徴量": data.feature_names, "回帰係数": lr_coefficients})
ridge_df = pd.DataFrame({"特徴量": data.feature_names, "回帰係数": ridge_coefficients})
lasso_df = pd.DataFrame({"特徴量": data.feature_names, "回帰係数": lasso_coefficients})

# 回帰係数を降順に並べる
lr_df = lr_df.sort_values(by="回帰係数", ascending=False)
ridge_df = ridge_df.sort_values(by="回帰係数", ascending=False)
lasso_df = lasso_df.sort_values(by="回帰係数", ascending=False)

# サブプロットの作成
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(12, 6))

# 重回帰モデルの係数プロット
ax1.barh(lr_df["特徴量"], lr_df["回帰係数"], color="skyblue")
ax1.set_xlabel("回帰係数の値")
ax1.set_ylabel("特徴量")
ax1.set_title("重回帰モデルの回帰係数")
ax1.grid(True)

# リッジ回帰モデルの係数プロット
ax2.barh(ridge_df["特徴量"], ridge_df["回帰係数"], color="lightgreen")
ax2.set_xlabel("回帰係数の値")
ax2.set_ylabel("特徴量")
ax2.set_title("リッジ回帰モデルの回帰係数")
ax2.grid(True)

# Lasso回帰モデルの係数プロット
ax3.barh(lasso_df["特徴量"], lasso_df["回帰係数"], color="salmon")
ax3.set_xlabel("回帰係数の値")
ax3.set_ylabel("特徴量")
ax3.set_title("Lasso回帰モデルの回帰係数")
ax3.grid(True)

plt.tight_layout()
plt.show()

アウトプットはこんな感じでした。

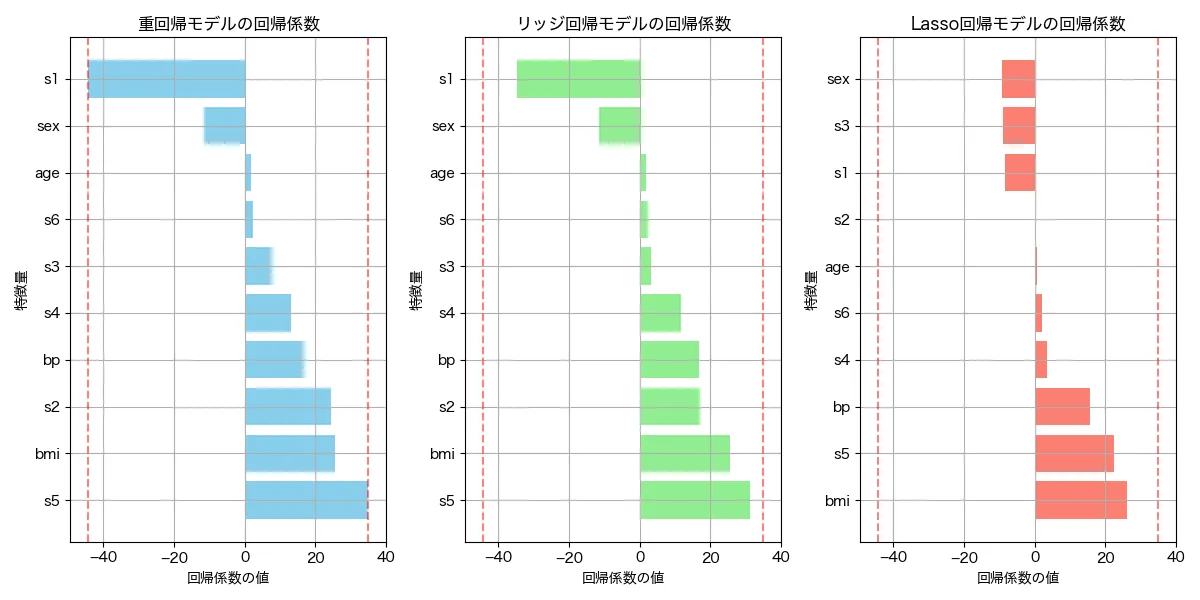
縦の赤い点線は、重回帰モデルの回帰係数の最小値と最大値となります。リッジ回帰もラッソ回帰も重回帰モデルの回帰係数の幅よりも小さくおさまっている様子がわかります。さらに、ラッソ回帰については「S1」や「age」と言った予測に不要な変数の係数が0に近づいていることがわかります。このように、正則化の効果が両モデルで出ていることがわかりました！

ちなみに、回帰係数のグラフの見方を簡単に見ていきましょう。

S1（血清総コレステロール）が正の方向に、S5（血清トリグリセリドレベル）が負の方向に、それぞれモデルの説明力に大きく貢献していることがわかります。つまり、血清総コレステロールが上がると糖尿病進行度が上がり、血清トリグリセリドレベルが上がると糖尿病進行度が下がる、ということがモデルから言えます。

ちなみに、通常、総コレステロール（S1）が高いことは動脈硬化や心血管疾患のリスクを高める ため、糖尿病の進行とも関連している可能性がます。また、トリグリセリド（S5）が高いことは糖尿病のリスクを上げると考えられており、この場合、「逆じゃねーか！」と思われます。ここら辺は僕も、医学の専門家でないので、全くわかりませんが、回帰係数は、「他の変数が一定だった場合に、当該変数が変化した場合の予測値の変化量」なので、通常、トリグリセリドが上がれば（両者に相関があるため）コレステロール値も上がるが、モデルではコレステロール値などの変数が一定だった場合のトリグリセリドの上昇に対する糖尿病リスクであり、その場合は糖尿病リスクは低いと言える、ということなのかもしれません。

リッジ回帰とラッソ回帰のαを変えた場合の実験

リッジ回帰とラッソ回帰では次のようにαの値を設定(alpha=xxx)してあげる必要があります。

# リッジ回帰モデル（α=1.0）
ridge = Ridge(alpha=1.0)

# Lasso回帰モデル（α=1.0）
lasso = Lasso(alpha=1.0)

じゃあ、どんな値にすればいいの？という疑問がでますよね。そこで簡単にαの設定によって、どんなふうに結果が変わるのか実験してみたいと思います。

α（正則化の強さ）を変化させたら、結果はどうなる？

リッジ回帰のαの様子

リッジ回帰の α（正則化パラメータ） を変えると、回帰係数の大きさや予測精度が変化します。αが 小さい ほど通常の線形回帰に近づき、αが 大きい ほど正則化が強くなり、回帰係数が抑制されます。

# フォント設定（Macの場合）
plt.rcParams["font.family"] = "Hiragino sans"

# αの値を変えてリッジ回帰を実行
alpha_values = [0.001, 0.01, 0.1, 1.0, 10, 100]
mse_values = []

for alpha in alpha_values:
    ridge_model = Ridge(alpha=alpha)
    ridge_model.fit(X_train_scaled, y_train)
    y_pred_ridge = ridge_model.predict(X_test_scaled)
    mse_values.append(mean_squared_error(y_test, y_pred_ridge))

# グラフ化
plt.figure(figsize=(8, 6))
plt.plot(alpha_values, mse_values, marker="o", linestyle="-")
plt.xscale("log")
plt.xlabel("正則化パラメータ α（対数スケール）")
plt.ylabel("MSE（平均二乗誤差）")
plt.title("α の変化によるMSEの変動")
plt.grid(True)
plt.show()

結果はこんな感じです。

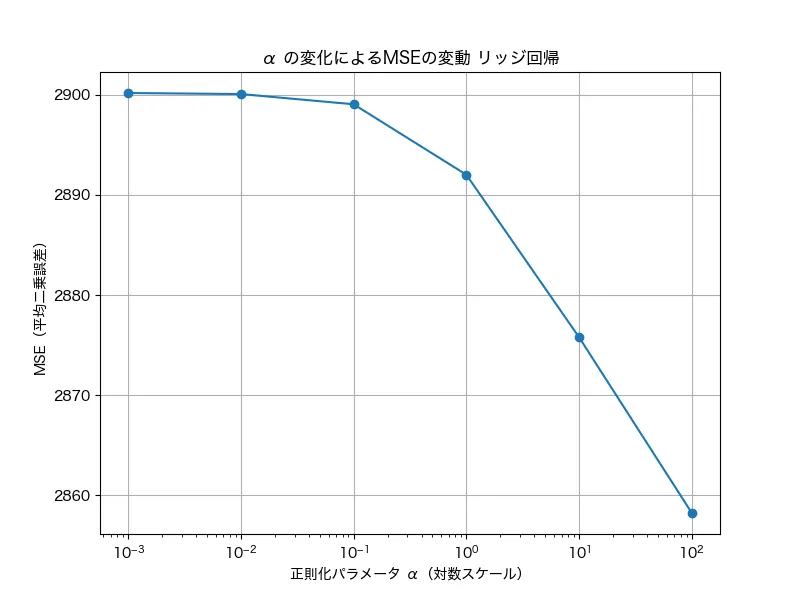
グラフでは10⁰ (=1.0)のところでガクッと下がっていますね。実際の分析場面でもこのようにざっくりとグラフを見ながら、現実場面では多くの場合、1未満で調整するといいでしょう。

ラッソ回帰のαの様子

同様にラッソ回帰でも実施したところ、以下のような結果でした。

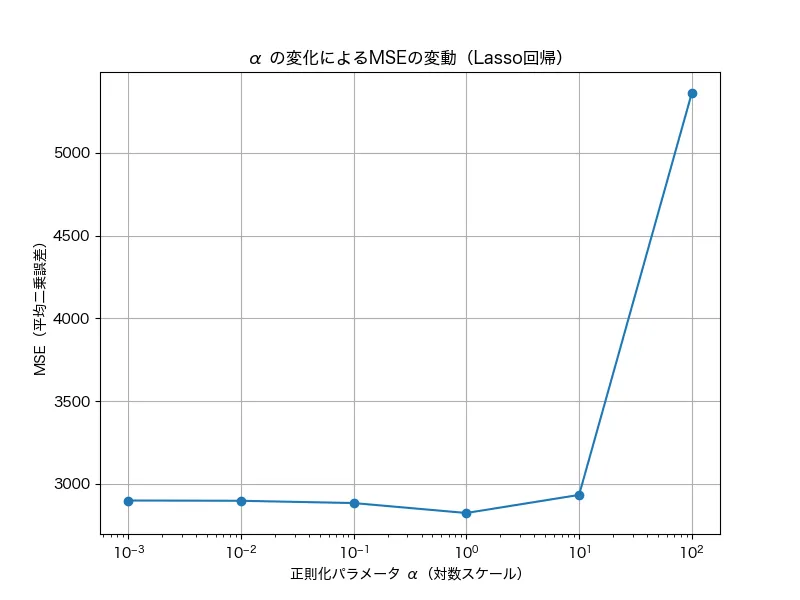
グラフでは、10⁰(つまり1)前後でMSEが最小になっているのがわかりますね。この結果からも、実装場面でも１前後（0.5~2くらい）で設定しながら、調整するのがいいでしょう。

特徴量ごとの係数の変化の確認

さらにαを変えた場合の回帰係数の変化についてもみてみましょう！

リッジ回帰のαと回帰係数の関係

リッジ回帰では αが増えると、回帰係数の大きさが抑制される ことが重要なポイントです。以下のコードで、 αを変化させたときの特徴量ごとの回帰係数の変動 を可視化します。

# フォント設定（Macの場合）
plt.rcParams["font.family"] = "Hiragino sans"

# αの値リスト
alpha_values = [0.001, 0.01, 0.1, 1.0, 10, 100]
coefs = []

# 各αで学習し、回帰係数を取得
for alpha in alpha_values:
    ridge_model = Ridge(alpha=alpha)
    ridge_model.fit(X_train_scaled, y_train)
    coefs.append(ridge_model.coef_)

# グラフ化
plt.figure(figsize=(10, 6))
for i in range(len(data.feature_names)):
    plt.plot(alpha_values, [coef[i] for coef in coefs], label=data.feature_names[i])

plt.xscale("log")
plt.xlabel("正則化パラメータ α（対数スケール）")
plt.ylabel("回帰係数の値")
plt.title("α の変化による回帰係数の変動")
plt.legend(loc="best", fontsize=10)
plt.grid(True)
plt.show()

結果はこんな感じです。

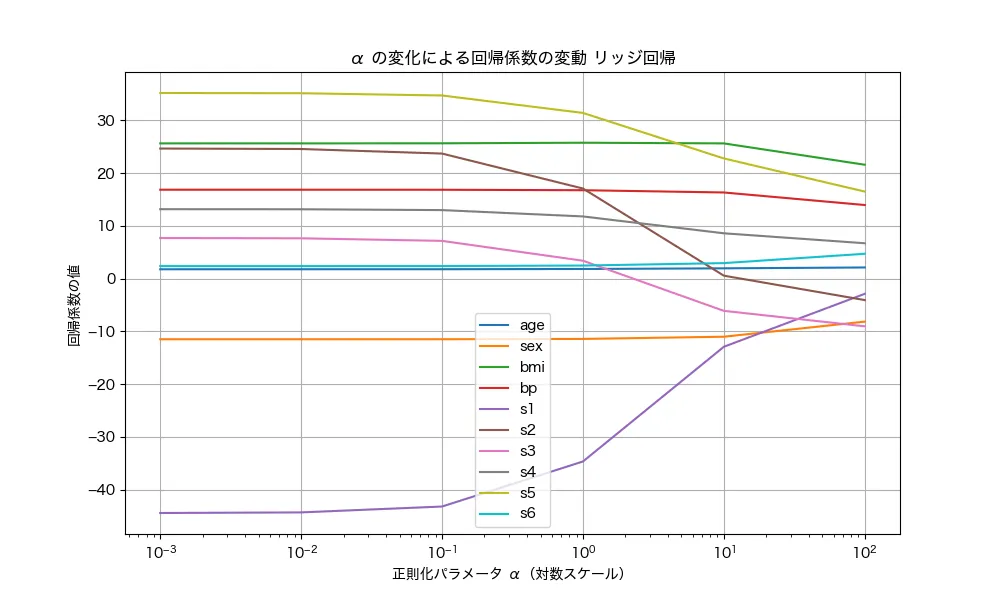
αを変化させた時、回帰係数の大きな特徴量ほど、ガクッと０に近くなっていますね。この正則化の影響で、大きな回帰係数ほど強くペナルティを受け、αの増加に伴い急激に0に近づく ことが見て取れます。この抑制の仕組みによって、過学習を防ぐ効果が期待できるんですね！

ラッソ回帰のαと回帰係数の関係

続いて、ラッソ回帰でもαの変化による回帰係数の変化をみてみましょう。

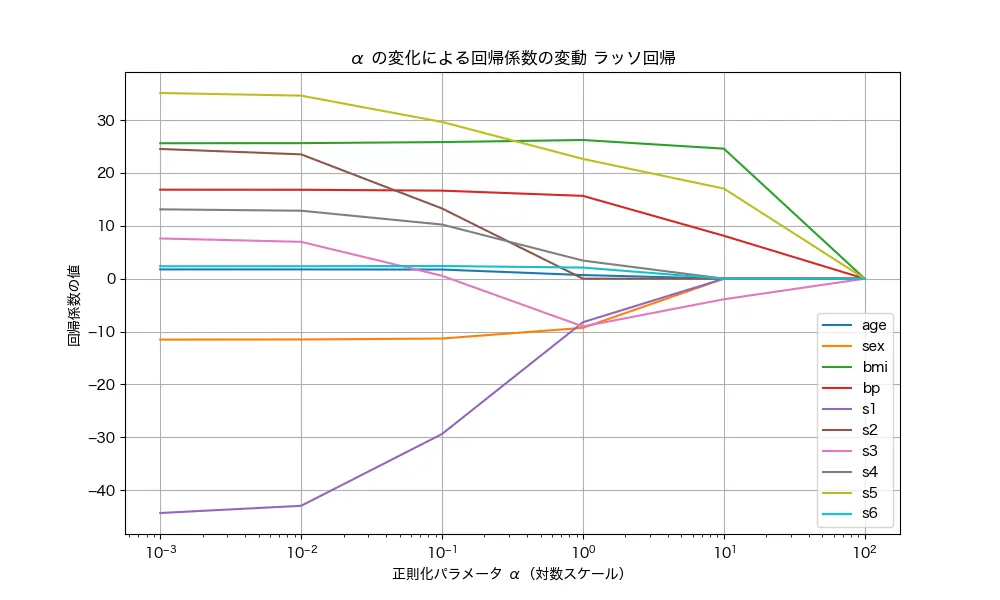
ラッソ回帰も回帰係数が小さくなるのは、リッジ回帰と一緒です。ただし、小さくなる様子はちょっと違いますね。まず、10² (つまり100)に設定すると全の回帰係数は０付近になっています。このことから、リッジ回帰はある幅に重みを押し込めるのに対して、ラッソ回帰は重みを0に減少させていく性質があると言えます。ただし、ラッソ回帰は全ての重みを均一に0に削減するのではなく、より重みの大きさが小さいものから０に減少させていく性質があります。あるいは、リッジ回帰はマイルドに重みを削減するのに対して、ラッソ回帰はガッツリと削減させる、というイメージでもいいかもしれませんね！

まとめ

以上が、リッジ回帰とラッソ回帰の解説でした。このモデルを使うことで、特徴量の影響を抑制する仕組みを、コードを用いて実感できたと思います！